|
|
|
Note to the Reader
This is a slightly expanded edition of a paper published in Optometry and
Vision Science June, 1999. The original and definitive print version is
available from OVS. This edition has full in-text citations. Please cite as:
Zhou G, Williams RW (1999) Mouse models for the analysis of myopia: an
analysis of variation in eye size of adult mice. Optometry and Vision
Science 76:408–418.
Email to: Guomin Zhou or Robert Williams HTML
Copyright © 1999 by RW Williams and G Zhou
Print Friendly
Mouse Models for the Analysis of Myopia: An Analysis of Variation in Eye
Size of Adult Mice
Guomin Zhou and Robert W. Williams
Center for Neuroscience, Department of Anatomy and Neurobiology,
University of Tennessee, 855 Monroe Avenue, Memphis, Tennessee 38163
Optometry and Vision Science: 408–418 (1999)
Abstract
To assess the relative importance of genetic and environmental factors
that modulate eye growth, eyes, lenses, and retinas of 507 mice belonging
to more than 50 strains were measured. Mice of both sexes and a wide range
of ages (27 to 526 days) were perfused for electron microscopy, and eyes,
lenses and retinas were dissected and analyzed. Our uniform fixation
protocol is associated with a weight loss of 4–6%. Multiple linear
regression methods were used to explore relations between eye and lens
weight, retinal area, age, sex, body and brain weight, and retinal
ganglion cell number.
The eye and lens of mice continue to grow long after sexual maturity
is reached at 40–60 days of age. The pace of growth matches the logarithm
of age. Despite their smaller bodies, females have eyes as large as those
of males. The correlation of eye weight to brain weight is remarkably low
(r= 0.19) while that to retinal area is high (r= 0.86).
Surprisingly, the correlation between lens weight and the size of the
posterior segment (eye weight minus lens weight) is only 0.5–0.6; and
ratios of these parameters are highly variable. Heritability of all traits
is between is 25–50%. The continued growth of eyes in adult mice provides
an excellent system to test effects of genetic and molecular manipulations
on the development and treatment of myopia. Heritability is sufficiently
high to map genes that specifically modulate growth of different parts of
the eye.
Introduction
Eye size in mammals varies a million-fold—from 1.1 mg in shrews to more
than 1.0 kg in humpback whales.1,2 The largest
eyes of all belong to giant squid. Their eyes attain an astonishing
diameter of 37 cm and a weight of 26 kg. 3 Most
of this variation between species can of course be accounted for by
differences in body size. However, significant variation remains even when
differences in body size are corrected: the ratio of eye weight to body
weight in 22 species of bats surveyed by Chase4
varies 40-fold—from a high of 0.2% in the white-lined bat Vampyrops
helleri to a low of 0.005% in Chilonycteris rubiquiosa.5
It follows that a subset of genes must target ocular tissues
selectively, modulating the rate and duration of eye growth separately
from that of the whole body. What is important from our point of view is
that genetic differences between species ultimately trace back to genetic
differences within species.6,7 There is a
reservoir of normal genetic variation within each species that influences
eye growth.8 Individuals inherit alleles that
predispose them to grow smaller or larger eyes under different sets of
environmental conditions.2,9–11
The genetic basis of this marked but perfectly normal variation in
eye growth has not yet been studied in any species. We do know that some
fraction of the variation in eye size is heritable, but we are only
beginning to identify genes that contribute to this variation. Eye growth
is not a trait controlled by one gene, but is a complex process governed
by a potentially large number of genes and environmental factors.8,12,13
Rapid advances in the past decade in molecular and quantitative genetics
now make it feasible to systematically identify single genes that modulate
eye growth, even when the individual effects of these genes are quite
small.14-16 For example, in recent work we have
successfully mapped four loci in the mouse that account for differences of
2–5% in eye weight.15,17,18 The genetic basis of
normal variation in eye growth is interesting in its own right, but it is
especially important given the critical impact that even slight
differences in eye size have on visual acuity in humans. Elongation of the
axial length of the eye by merely 1 mm without other compensation will
result in a myopia of 2.0–2.5 diopters.19
Given the central role of the mouse in biomedical and genetic
research, the advantages of using this species for studying eye
development are numerous. The genetic map of this species has been well
characterized; mice are easy to breed; and there are numerous ways to
manipulate their genes. An important reservation is that mice are a
nocturnal species with a visual system that differs markedly from that of
humans. They have a rod-dominated retina and comparatively poor visual
acuity. Despite these key differences, we should not discount the utility
of mice in studying eye growth, nor should be discount the reliance that
they themselves place on vision. As a fraction of total body size, the
mouse eye is approximately 10 times larger than the human eye.20
Our aim in this study is to analyze environmental and genetic
factors that contribute to normal differences in growth of the eye, lens,
and retina of mice. We address the following types of questions: To what
degree is normal variation in eye size heritable? How much of the
variation is due to such factors as sex, age, and body size? How tightly
coupled are the growth of eye, lens, and retina? In this study we begin
with a survey of variation in eye size in numerous strains of mice. We
summarize data on the correlations between body weight, age, and sex and
the size of the eye, lens, and retina. The reader who is not familiar with
statistical analysis and multiple regression analysis in particular may
find our results burdensome, but this type of quantitative analysis of
sources of variation in eye size is an absolute prerequisite. This
analysis is a foundation for further work on genetic and environmental
control of normal eye growth in mice and humans.
METHODS
Animals
Eyes were taken from a total of 507 mice belonging to different
subspecies, strains, and substrains (Table 1). Most animals used for
breeding were obtained from the Jackson Laboratory, Bar Harbor, Maine. The
strains CAST/Ei and CASA/Rk are inbred members of the subspecies Mus
musculus castaneus; whereas MOLC/Rk and MOLF/Ei are inbred members of
the subspecies Mus musculus molossinus. All other strains and
substrains are standard inbred laboratory strains. Seven strains (BXHA1/Sr,
BXHA2/Sr, BXHB2/Sr, BXHC2/Sr, BXHD1/Sr, BXHE1/Sr, and BXHE2/Sr) were
provided to us by Dr. Linda Siracusa. These recombinant inbred strains are
based on a cross between C57BL/6J and C3H/HeJ, and were between their 11th
and 17th generations of successive filial mating. The nomenclature we have
used for these particular strains in provisional. For the derivation and
relations among strains see
nervenet.org/papers/images/other/StrainLineage.gif.
The mix of sexes among strains varied, but the sex ratio across all
strains was close to 1:1 (264 males, 243 females). As will become evident
in the Results section, sex is not a critical variable. The age of
mice ranged from 27 to 526 days. Most animals were fed a 6% fat NIH31 diet
at the Jackson Laboratory and a 5% fat Agway Prolab 3000 rat and mouse
chow at the University of Tennessee. Colonies were maintained at 20–24 °C
on a 14/10 h light-dark cycle in a pathogen-free environment.
The rd1 nonsense mutation in the phosphodiesterase beta gene
(symbol Pdeb, located on mouse chromosome 5 at 57 centiMorgans)
causes photoreceptors to die during the first four weeks of life (reviewed
at
www.informatics.jax.org/bin/fetch_mlc?12235). This mutation is
unfortunately extremely common among inbred strains,21
and 15 of the 50 strains that we studied were known to be rd1
homozygotes. These rd1 strains are indicated in Table 1. The seven
new BXH strains we obtained from Dr. Siracusa were uncharacterized with
respect to rd1. To assess whether or not these strains carry the
rd1 allele we genotyped the markers D5Mit239 and D5Mit403
that closely flank Pdeb on Chr 5 (see
nervenet.org/papers/PCR.html for technical details). If both alleles
at both markers are inherited from the C3H/HeJ parent known to carry the
rd1 mutation, then it is almost certain that the derivative inbred
strain will lack rod photoreceptors. We also examined unstained retinal
wholemounts of these mice under Nomarski optics to verify their
photoreceptor phenotype (present or absent).
We have found (R. W. Williams and G Zhou, in progress) that the
deleterious effects of the rd1 mutation are not restricted entirely
to retina. Mice that are homozygotes for this mutation have normal lens
weight, but overall eye size is reduced significantly. We divided our
dataset into pools with and without the rd1 mutation to determine
whether key observations depend on this particular gene product.
Except where noted, values provide in the Results section are
either insensitive to the inclusion of animals with rd1 or are
given for wildtype mice only.
Fixation
All mice reported in this study were anesthetized with Avertin (0.5–1.0
ml ip), were weighed to the nearest 0.1 mg, and were perfused with 0.1 M
phosphate buffered (PB) saline followed by 1.25 glutaraldehyde and 1.0%
paraformaldehyde in 0.1M phosphate buffer, followed by 2.5% glutaradehyde
and 2.0% paraformaldehyde in 0.1 M PB. The total duration of perfusion was
approximately 3–5 minutes. Eyes were removed from each mouse. Optic nerves
and extraocular muscles were cut away. Weights are expressed as the
average weight of left and right eyes.
Assessment of fixation effects. All of the original weight
data were taken from perfusion fixed specimens used in an extensive
analysis of the retinal ganglion cell population in mice.22,23
While the perfusion and fixation techniques were uniform,
raw fixed weight of eyes and lenses will clearly differ from in vivo or
unfixed values. To assess the effects of fixation we compared fixed and
unfixed eye weights in an independent set of 340 animals of different
genotypes. (The 340 animals used to assess fixation affects are not
otherwise included in this study and are not described in the Results
section.) After anesthetizing these mice, their right eyes were
immediately enucleated, cleaned and weighed, often within an interval of
two to five minutes. These weights provided a reference. The freshly
enucleated right eyes were then place in same fixative used for the
perfusion. While one investigator prepared the right eye, the mouse was
perfused by the other investigator. The perfusion fixed left eyes were
subsequently dissected and weighed. Weights of perfused eyes were compared
to those of the right eye prior to fixation. Weights of perfusion fixed
eyes stored in our standard 0.1 M PB were generally 1 to 2 mg (6%) less
than those of freshly extirpated unfixed eyes. However, there was no
significant difference between weights of perfusion fixed eyes and
unperfused right eyes after fixation by immersion. A comparable analysis
was carried out to assess the effects of fixation on the weight of the
lens. Fixed lenses typically weigh 0.2–0.3 mg (3–5%) less than those of
unfixed lenses. This analysis demonstrated that there was a consistent,
but slight decrease in weight after fixation. Assuming constancy of
proportion, a 6% decrease in weight corresponds to a 2% decrease in linear
measures. In conclusion, fixation with the high-grade fixatives used for
electron microscopy has a modest and consistent effect on ocular
parameters. Values of individual mice plotted in Figures 1 and 2 are
original fixed eye weights without adjustment for fixation effects.
However, strain average data (Figures 3 and 4, and Table 1) for eye and
lens weights have been adjusted upward 6% and 4% respectively, to correct
for fixation effects. These adjusted values will be very close to means of
unfixed enucleated samples.
Retinal wholemounts
The cornea was cut off of the eye and six 1–2 mm radial incisions were
made through the entire eyecup from the corneal limbus toward the optic
nerve head. In more than 90% of all cases, wholemounts were prepared from
the left retina. Retinas were carefully separated from the choroid and
sclera and mounted on slides in a polyvinyl alcohol and glycerol solution.24
Orientation of retinas was determined by reference to patterns of
choroidal vessels. Tracings of flattened retinas were drawn at low power
using a drawing tube on a microscope. Retinal area was measured with a
digitizing tablet interfaced to a Macintosh computer.
Regression analysis
Eye weight varies with age, sex, and body weight. This presents a
problem in comparing eye weights of different strains of mice since each
strain may include different numbers of males and females, animals of
different ages, etc. Multiple linear regression was performed to
investigate relationships among these variables, and to reduce unwanted
effects on these factors when comparing strains. Data on size, age, sex,
and body weight were available for almost all animals. Eye weight
increases linearly as a function of the logarithm of age and for this
reason we used log-transformed age data in the regression analysis.
Exploratory analysis and multiple linear and non-linear regression were
carried out using the program DataDesk 6 (Data Description Inc., Ithaca
NY). In general, we have normalized data on eye weight to that expected of
22-gm females at an age of 75 days.
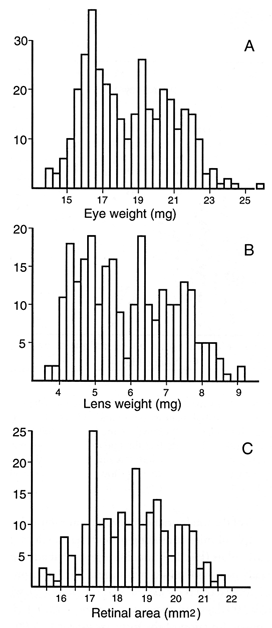
FIGURE 1. (A) Eye weight of a sample of 372 adults. Both eyes from
each animal were weighed and averaged. The histogram shows the full range
of variation and data are shown without compensation for difference in
age, sex, and body weight. All animals with retinal degeneration were
excluded. (B) Corresponding data for a subset of lenses from 259 cases.
Each data point is average of both eyes. (C) Corresponding histogram for a
subset of retinal areas from 215 cases. In general, wholemounts were only
prepared from the left eye. Values are not corrected for the small effects
of fixation.
Heritability
Broad sense heritability was computed using Hegmann and Possidente's
equation25
where V A
is the variance among strains and VE
is the average environmental variance within isogenic strain. Broad-sense
heritability, or genetic determination, is a relative measure of the
fraction of variance due to the combination of all genetic factors
(additive, dominance, and epistasis). The four wild subspecies and rd1
strains were excluded from the analysis of heritability.
Table 1. Strain variation in the mouse eye
|
Strain |
Eye Weight
±SE(mg) |
Lens Weight
±SE(mg) |
Retinal area
±SE(mm2) |
RGCb
(x1000) |
Range
Nc |
| 129/J |
17.6 |
±0.5 |
5.97 |
±0.06 |
17.5 |
±0.2 |
63.8 |
±1.8 |
5 |
| 129/SvJ |
19.1 |
±0.3 |
5.56 |
±0.09 |
18.5 |
±0.1 |
69.1 |
±5.4 |
5–10 |
| A/J |
18.1 |
±0.3 |
5.94 |
±0.17 |
17.1 |
±0.5 |
50.6 |
±1.3 |
5–15 |
| AKR/J |
19.3 |
±0.3 |
5.65 |
±0.18 |
19.0 |
±0.2 |
62.8 |
±0.9 |
6 |
| BALB/cByJ |
18.2 |
±0.3 |
5.61 |
±0.12 |
17.4 |
±0.1 |
55.9 |
±1.2 |
6 |
| BALB/cJ |
18.9 |
±0.1 |
5.45 |
±0.19 |
18.3 |
±0.5 |
63.4 |
±2.3 |
6–18 |
| C57BL/6J |
19.0 |
±0.1 |
5.84 |
±0.15 |
18.5 |
±0.2 |
55.4 |
±0.8 |
16 |
| C57BL/10J |
19.1 |
±0.2 |
5.58 |
±0.04 |
18.7 |
±0.1 |
– |
5–10 |
| C57BLKS/J |
20.8 |
±0.2 |
6.62 |
±0.18 |
19.5 |
±0.1 |
65.7 |
±1.9 |
11 |
| C57L/J |
20.0 |
±0.6 |
5.94 |
±0.12 |
20.0 |
±0.3 |
53.1 |
±5.9 |
5–6 |
| C58/J |
20.1 |
±0.2 |
5.87 |
±0.07 |
20.1 |
±0.1 |
– |
9 |
| CASA/Rk |
19.1 |
±0.3 |
6.12 |
±0.13 |
18.7 |
±0.4 |
47.2 |
±1.4 |
4–8 |
| CAST/Ei |
19.7 |
±0.3 |
5.73 |
±0.11 |
18.3 |
±0.1 |
45.1 |
±1.0 |
8 |
| CBA/CaJ-rd |
18.9 |
±0.2 |
5.48 |
±0.07 |
19.1 |
±0.2 |
56.0 |
±1.2 |
6 |
| CE/J |
18.7 |
±0.3 |
6.34 |
±0.19 |
17.7 |
±0.4 |
63.6 |
±2.5 |
7 |
| C3H/HeJ-rd |
18.2 |
±0.4 |
6.10 |
±0.05 |
18.1 |
±0.1 |
68.2 |
±3.5 |
9–10 |
| C3H/HeSnJ |
19.0 |
±0.4 |
6.37 |
±0.10 |
18.4 |
±0.2 |
67.8 |
±1.7 |
9–10 |
| DBA/1J |
18.9 |
±0.4 |
5.64 |
±0.16 |
18.2 |
±0.1 |
– |
10 |
| DBA/2J |
20.1 |
±0.3 |
5.79 |
±0.14 |
19.5 |
±0.5 |
63.4 |
±1.2 |
8–20 |
| LG/J-rd |
17.9 |
±0.3 |
5.49 |
±0.15 |
17.8 |
±0.3 |
61.6 |
±3.2 |
6–12 |
| LP/J |
19.2 |
±0.3 |
5.95 |
±0.14 |
19.0 |
±0.4 |
52.2 |
±2.0 |
6–7 |
| MOLC/Rk |
18.8 |
±0.4 |
6.30 |
±0.16 |
18.5 |
±0.4 |
– |
5 |
| MOLF/Ei |
16.8 |
±0.3 |
5.10 |
±0.09 |
17.2 |
±0.1 |
– |
6 |
| NOD/LtJ |
19.2 |
±0.2 |
5.77 |
±0.05 |
19.1 |
±0.1 |
– |
10–15 |
| NZB/BinJ |
17.5 |
±0.5 |
5.42 |
±0.19 |
17.1 |
±0.5 |
61.1 |
±1.6 |
5 |
| NZW/LacJ |
19.4 |
±0.2 |
6.11 |
±0.11 |
19.9 |
±0.1 |
63.7 |
±0.7 |
5 |
| PL/J-rd |
17.3 |
±0.2 |
5.53 |
±0.03 |
18.4 |
±0.5 |
56.0 |
±1.3 |
5 |
| SJL/J-rd |
16.8 |
±0.2 |
5.26 |
±0.07 |
16.0 |
±0.3 |
52.5 |
±1.8 |
7 |
| SM/J |
19.0 |
±0.1 |
6.21 |
±0.11 |
19.2 |
±0.2 |
65.8 |
±4.7 |
4–25 |
| SWR/J-rd |
17.9 |
±0.1 |
5.81 |
±0.09 |
17.4 |
±0.5 |
63.2 |
±2.9 |
6–9 |
| BXH2-rd |
18.9 |
±0.4 |
6.35 |
±0.12 |
17.9 |
±0.5 |
64.6 |
±1.8 |
6 |
| BXH3-rd |
18.1 |
±0.3 |
6.31 |
±0.13 |
17.4 |
±0.3 |
63.0 |
±2.1 |
9–10 |
| BXH4-rd |
18.4 |
±0.2 |
5.95 |
±0.15 |
17.9 |
±0.3 |
67.0 |
±3.0 |
10–13 |
| BXH6-rd |
19.0 |
±0.2 |
6.36 |
±0.04 |
18.4 |
±0.4 |
52.3 |
±1.3 |
8–15 |
| BXH7-rd |
18.3 |
±0.1 |
6.14 |
±0.09 |
17.8 |
±0.2 |
57.9 |
±2.7 |
8–9 |
| BXH8-rd |
17.6 |
±0.3 |
5.85 |
±0.11 |
17.7 |
±0.1 |
62.4 |
±2.2 |
8–9 |
| BXH9-rd |
17.4 |
±0.2 |
6.10 |
±0.07 |
16.8 |
±0.2 |
57.5 |
±1.6 |
7–20 |
| BXH10 |
18.6 |
±0.3 |
5.94 |
±0.17 |
17.9 |
±0.3 |
57.1 |
±2.6 |
7–8 |
| BXH11 |
19.9 |
±0.2 |
6.25 |
±0.12 |
18.7 |
±0.3 |
55.0 |
±1.7 |
8–11 |
| BXH12 |
21.6 |
±0.2 |
6.62 |
±0.16 |
20.6 |
±0.2 |
69.5 |
±0.9 |
7–15 |
| BXH14-rd |
18.6 |
±0.2 |
6.45 |
±0.09 |
17.9 |
±0.1 |
68.2 |
±1.9 |
8–10 |
| BXH19-rd |
18.7 |
±0.2 |
5.95 |
±0.16 |
17.3 |
±0.2 |
52.2 |
±4.0 |
8–10 |
| BXHA1/Sr |
19.5 |
±0.3 |
6.06 |
±0.12 |
19.5 |
±0.2 |
– |
6–8 |
| BXHA2/Sr |
19.2 |
±0.4 |
5.58 |
±0.12 |
18.9 |
±0.4 |
– |
6–9 |
| BXHB2/Sr-rd |
19.5 |
±0.4 |
5.51 |
±0.25 |
18.3 |
±0.7 |
– |
5–9 |
| BXHC2/Sr-rd |
19.5 |
±0.4 |
5.56 |
±0.11 |
19.0 |
±0.3 |
– |
5–17 |
| BXHD1/Sr |
19.0 |
±0.6 |
5.59 |
±0.24 |
18.8 |
±0.8 |
– |
5–10 |
| BXHE1/Sr |
20.2 |
±0.6 |
5.64 |
±0.11 |
19.4 |
±0.3 |
– |
5–10 |
| BXHE2/Sr |
19.9 |
±0.4 |
6.11 |
±0.13 |
19.4 |
±0.4 |
– |
5–10 |
| BXD5 |
19.6 |
±0.2 |
6.06 |
±0.15 |
19.0 |
±0.2 |
75.6 |
±1.3 |
8–18 |
a Fresh eye weight and lens weight after correction by
multiple regression for differences in age, sex, and body weight. All
cases normalized to values expected of a 75- day-old, 22-gm female.
b Retinal ganglion cells
c Number of eyes and lens weighed. Usually 5 to
12 retinal wholemounts were prepared.
RESULTS
With rare exceptions, eyes of adult mice weigh from 14 mg to 24 mg
(Fig. 1A). Lenses weigh from 3.7 to 8.7 mg (Fig. 1B). This is an
extraordinary level of variation and the immediate question is whether
this variation is due to age, sex, body size, or genetic differences. Much
of the following analysis in this section is directed at determining the
source of this variation using linear regression analysis.
Average fixed weights of the eye and lens for all cases are 17.8 ±
0.1 mg SE (n= 503) and 5.75 ± 0.06 mg (n= 369),
respectively. Corresponding values after correction for fixation are 18.8
mg and 5.91 mg. When animals with retinal degeneration are eliminated from
the sample (Fig. 1), the average eye weight rises to 18.4 ± 0.1 SE (n
= 366, 19.4 mg unfixed), whereas mean lens weight rises to 5.91 ± 0.08 mg
(n= 258). For both of these traits the histograms have a
distribution that appears bimodal (Fig. 1A, B). This bimodality is
actually due to an underlying bimodal age distribution—young adults in one
mode, retired breeders in the other mode. When regression analysis is used
to compensate for age differences, the bimodality disappears. Retinal area
in normal rd-free mice ranges from 15.5 to 21.5 mm 2
and the distribution is more nearly normal in shape (Fig. 1C).
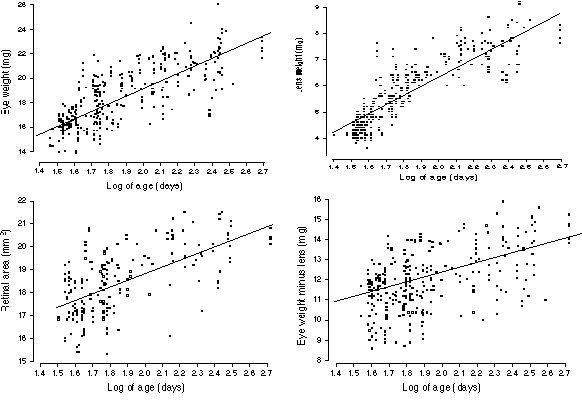
FIGURE 2. Age effects on the eye, lens, and retina. (A) Growth of
the eye from 40 days (or 1.6 log days on the x axis) to 400 days (2.6
log). The rate of growth declines steadily as a function of the logarithm
of age. Nonetheless, there is a significant gain between sexual maturity
(40 days) and old age (400 to 600 days). This plot only includes cases
free of retinal degeneration. The line of best fit is drawn through the
data set (B) Growth of the lens in adult mice. The slope is greater than
that for eye growth, nearly doubling lens weight over the life of a mouse.
Note in this case that the line of best fit does not accurately reflect
the two phases of lens weight gain (see text). The rd1 alleles do
not affect lens size, and this plot includes strains that carry this
mutation. (C) A plot of the effects of age on the non-lenticular part of
the eye. Unlike the lens itself, the variable eye minus lens shown
here is does not suggest early and late phases of growth. (D) Growth of
the retina with age. Values are not corrected for the small effects of
fixation.
Age
The size of the eye and lens increase almost logarithmically from 30 to
300 days of age (Fig. 2A and B). A simple equation adequately describes
eye growth: eye weight (mg) = 6.1 + 6.4 (log of age in days).
Remarkably, this simple equation accounts for approximately 60% of the
total variance in eye weight even among a highly diverse sample of mice
consisting of both sexes. Closer inspection of the scatter plots (Fig. 1A,
B) suggests that adult eye growth may actually be divisible into stages.
The equation for young adults (27 to 99 days) is eye weight = 1.2 +
9(log age), whereas that for animals 100 days and above is eye
weight = 13.5 + 3.2(log age). A single power function of the form
eye weight = 9.06 + age0.156 fits the entire
age range well.
Lens weight is also highly predictable on the basis of age (Fig.
2B). In fact, 74% of all variance in lens weight is accounted for using
the simple equation lens weight (mg) = 3.6 (log age) – 1.0. The two
phases of growth mentioned above are more prominent in the plot of the
lens data (Fig. 2B). Coefficients for younger (<100 days) and older
animals are 5.85 ± 0.26 SE and 1.28 ± 0.40, respectively.
We performed a regression analysis of the parameter eye–lens
weight and this parameter gave a better fit using a simple log-linear
function (Fig. 2C): eye minus lens (mg) = 7.4 + 2.6 (log age). This
finding points to an interesting difference in the pace with which
different parts of the eye grow in adult mice. The lens grows most rapidly
between 30 and 100 days, but thereafter the pace is retarded. In contrast,
the non-lenticular components of the eye grow at a rate that is more
nearly a function of the logarithm of age between 30 and 500 days. For
these non-lenticular components, the decline in the coefficient is quite
modest—from 3.22 ± 0.67 (SE) for younger adult to 1.83 ± 0.83 for animals
older than 99 days. Naturally, on a standard non-logarithmic plot all of
these parameters would reveal a progressive reduction in the pace of
growth.
Finally, retinal area also increases with age (Fig. 2D). However,
only 40% of the variance in retinal surface area can be explained by age
alone. The best linear fit is retinal area (mm2)
= 12.5 + 3.3 (log age). All equations listed above are either
insensitive to, or are fully corrected for, effects of the rd1
mutation.
Body size
How closely coupled are growth of the eye and that of the body? Could
the age-related gain in eye size simply reflect an increase in body size?
To answer these types of questions we performed multiple linear
regression. As expected, and as shown in Table 2, age and body weight are
positively correlated (r= 0.5). After correcting for age and sex
differences, it is clear the body size in isolation still has a
statistically significant, if small, effect on eye size. The regression
coefficient, or slope, amounts to a gain of 0.17 ± 0.02 mg SE in eye
weight for a one gram increase in body weight.
A corresponding analysis of lens weight and retinal area also
reveals consistent but small effects of body size. The slope is 0.054 ±
0.013 mg per gram body weight (p < 0.0001). Retinal area keeps
pace, gaining 0.07 ± 0.02 mm2 per gram body
weight (p = 0.004). These coefficients are approximately those
expected from the differences in total eye weight; in other words,
differences in body weight are associated with matched differences in the
size of the eye, lens, and retina.
We can now reverse the question posed above and ask what the
age-related effect on eye size is when we remove the confounding effects
of changes in body weight. The short answer is that correcting for body
weight depresses coefficients slightly. For example the coefficient of 6.4
quoted in the lead paragraph on effects of age is reduced to 4.7.
Corresponding coefficients for the lens drop from 3.6 to 3.1 and for
retina from 3.3 to 2.5. In every instance, age is a more important
predictor than body weight.
Sex
There are intriguing sex differences in humans in the size of the lens,26
and therefore, presumably also in the total size of the eye. These
differences are likely to trace back to marked sexual dimorphism in body
size. Male and female mice also differ in body size (10—15%), and using
our dataset we can assess sex-specific contributions to differences by
factoring out body size. Without any corrections at all, the mean eye
weight of male mice free of rd is 18.32 ± 0.18 mg (SE), whereas
that of female mice is 18.40 ± 0.19 mg. Comparable values for the lens are
5.86 ± 0.11 and 5.95 ± 0.12 mg, and those for retinal area are 18.33 ±
0.14 and 18.56 ± 0.14 mm2. Despite a large n,
these differences are insignificant. Male mice weighed ~12% more than the
females (23.0 versus 20.6 gm). Thus, when an adjustment is made for this
body size difference, eyes of females are proportionally larger than those
of males (p = 0.001). The multiple regression equation has the
simple form eye weight = 0.3 (body weight) + 0.75 mg if female.
When the regression analysis is broadened to factor out differences
in age, brain weight, and retinal ganglion cell number, the isolated
effect of sex is 0.6 mg (p = 0.03). From this we predict that
male-female littermates with the same body weight will have eye weight
differences amounting to about 3%. The corresponding sex difference in the
weight of the lens is 0.35 ± 0.11 mg (6.1%, p = 0.002). Finally,
there is no difference in retinal area, either in absolute terms or in
comparative terms after multiple regression analysis. This observation is
consistent with our previous electron microscopic analysis of the retinal
ganglion cell population in mice, in which no sex difference was noted in
a sample of several hundreds of mice.22
Correlations
We have acquired data on several variables in many of the same strains
and individuals for which we now present data on eye, lens, and retina
(see
nervenet.org/main/databases.html). Table 2 summarizes associations
among these variables for individual wildtype mice. The upper right region
lists Pearson product-moment correlations, whereas the lower left region
lists the amount of explained variance (the coefficients of determination,
r2, expressed as a percentage). With the
exception of data on retinal ganglion cell number, correlations are based
on comparisons among more than 200 mice, and r values in Table 2
above 0.14 are statistically significant (p < 0.05). For the
retinal ganglion cell data (df = 37), only correlations above 0.32
are significant. Of 28 correlations in the table, the great majority are
significant–almost all at p < 0.001. Three correlations involving
ganglion cell number (cell number vs. age, vs. body weight, and vs. lens
weight) are not significant. One especially interesting finding is that
the correlation between lens weight and the weight of the remainder of the
eye is 0.59. Thus only 35% of the variance in lens weight can be predicted
by variation in the weight of the rest of the eye! The correlation between
eye size and brain weight is also quite low (r = 0.42), and only
17% of the variance in eye size can be predicted from differences in brain
weight.
Table 2. Correlation matrix for eight key parameters
| |
Age |
Eye |
Eye—Lens |
Lens |
Retina |
RGC |
Brain |
Body |
| Age |
— |
0.80 |
0.56 |
0.86 |
0.63 |
-0.04 |
0.20 |
0.54 |
| Eye |
63% |
— |
0.90 |
0.89 |
0.86 |
0.35 |
0.35 |
0.66 |
| Eye—Lens |
30% |
81% |
— |
0.59 |
0.80 |
|
0.35 |
0.53 |
| Lens |
72% |
78%; |
35% |
— |
0.77 |
-0.11 |
0.22 |
0.61 |
| Retina |
40% |
74% |
64% |
59% |
— |
0.37 |
0.20 |
0.44 |
| RGC |
0% |
13% |
30% |
1% |
14% |
— |
0.24 |
-0.14 |
| Brain |
4% |
12% |
12% |
5% |
4% |
6% |
— |
0.49 |
| Body |
29% |
43% |
28% |
38% |
19% |
2% |
24% |
— |
In the upper-right half of this table are the correlations the
eight variables: 1. age, 2. eye weight, 3. eye weight minus lens weight,
4. lens weight, 5. retina area, 6. retinal ganglion cell number (RGC), 7.
brain weight, and 8. body weight. All correlation were computed from
strain averages (n= 30 rd1-free strains). To the lower left
are the coefficients of determination (r2)
expressed as percentages. These percentages provide a way to assess how
much of the variance in one trait, for example eye weight, is explained by
variation in another trait, for example, body weight. For this pair (eye
and body weights) 43% of the variance in eye weight can be "explained" by
variation in body weight.
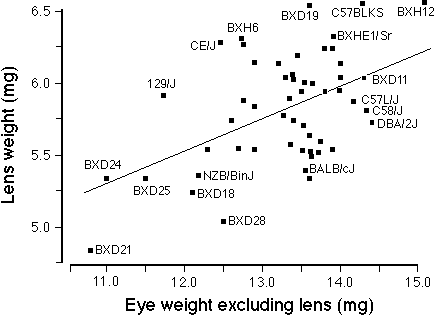
FIGURE 3. Correlation between lens weight and the remainder of the
eye (eye minus lens) for a set inbred strains of mice. This
includes the 28 rd1-free strains from this study and the BXD
strains described in Zhou and Williams. 17 The
wild species of mice, MOLC/Rk and MOLF/Ei, were excluded. The least-square
linear regression line is drawn. There is very wide scatter about the line
of best fit and the correlation is only 0.5. This suggests considerable
strain differences in the regulation of eye and lens growth.
Correlations among strain averages were computed using a combined
dataset consisting of the 30 strains free of retinal degeneration in this
study and 25 BXD strains tabulated in Zhou and Williams17
( their Table 1). Figure 3 shows that the correlation between the weight
of the lens against the remainder of the eye (eye weight excluding lens)
is only 0.50. Only 25% of the variance in lens weight can be predicted
from the weight of the remainder of the eye. This validates the low
correlation obtained from the analysis of individual mice in the preceding
paragraph. The correlation between lens and retina is somewhat
higher–approximately 0.58. These comparatively low correlations imply a
surprising degree of independence in the genetic control of eye and lens
growth in mice.
Combining Factors
To what extent can the size of the eye and lens be predicted from
easily obtained information on body weight, sex, age, brain weight, etc.?
What are the relative predictive powers of these variables? The answer is
that 70–75% of all variance in eye size can be accounted by age, body
weight, and brain weight.
Sex is unimportant. The logarithm of age has 2.5 times the
predictive power of body weight, which in turn has 2.5 times the
predictive power of brain weight (t ratios of the regression
analysis are 17.5, 7.0, and 2.4, respectively). The best equation for mice
free of rd1 is eye weight (mg) = 4.5 + 5 (log age) + 0.12 (body
weight in gm) + 4.3 (brain weight in gm). A 100-day-old mouse that
weighed 25 gm and that had a 0.465 gm brain would be expected to have eyes
that weighed about 19.5 mg.
Lens weight is more reliably predicted than eye size using just age
and body weight. The equation lens weight (mg) = 3 (log age) + 0.56
(body weight in gm) – 1.07 accounts for 78% of the variance. The
logarithm of age has three times the predictive power as does body weight,
and neither sex nor brain weight are significant predictors of lens
weight. In contrast, retinal area cannot be well predicted using these
variables. Age, body, sex, and brain only account for 42% of the variance
and only the former two parameters are significant. The equation is
retinal area in mm2 = 12.7 + 2.5 (log age) +
0.05 (body weight in gm).
Strain variation
All of the strains listed in Table 1 are genetically uniform or
isogenic. For this reason, differences within strain are almost entirely
due to non-genetic developmental and environmental factors, whereas
differences between strains are due primarily to genetic factors. After
compensating for differences associated with age and body weight all three
traits vary relatively modestly–the range between lowest and highest
values amounts to only 20–30%. Strain average eye weight ranges from 16.0
± 0.2 to 21.6 ± 0.2 mg (Table 1); lens weight ranges from 5.2 to
6.6 mg; and retinal area ranges from 17.1 to 20.6 mm2.
These ranges are narrowed only slightly when mice with rd1 are
excluded.
Probability density plots were constructed from the rd1-free
strain averages. These plots are analogous to smoothed histograms of the
data but instead of adding bars, normal distributions are added. If a
collection of strains has a multimodal probability density plot, then this
suggests that one or two genes have major effects.17,22
Figure 4 shows that the distribution of eye weights of those 30 strains
that are free of rd1 is unimodal, sharply peaked at 19 mg, and
somewhat skewed. This pattern does not suggest that a single gene locus
has a strong effect.
Heritability
Broad-sense heritability was computed after correcting for age, sex,
and body weight differences. Variation in eye weight has a heritability of
31%, lens weight of 25%, and retinal area of 41%. Note that these
estimates are depressed slightly by technical error but are probably
increased significantly by the homogeneous pathogen-free environment in
which mice were raised. The heritability estimates have a sampling error
of approximately ±5%.
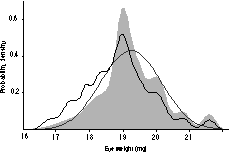
FIGURE 4. Probability density plot for eye weight data (gray
curve). This plot is a visual description of the variation in eye size
in Table 1, and incorporates data from rd1-free strains. The wild
strains MOLC/Rk and MOLF/Ei were excluded. The smooth normal distribution
is based on the mean and standard deviation among strain averages. The
other irregular function (fine dark line) shifted slightly to the left is
the probability density for all strains listed in Table 1.
DISCUSSION
Synopsis. Our aim has been to provide reliable baseline data on
eye weight in mice as a prelude to developmental and genetic analysis. By
pooling data from such a wide variety of strains we can be confident that
robust and general relationships will be detected. We have also examined
strains in isolation to identify those that have unusually large and small
eyes, lenses, and retinas. The extreme strains are of great utility in
gene mapping studies. We hope that some of these striking differences
between strains (Table 1, Fig. 3) will entice those interested in the
origins and treatment of refractive error to explore mechanics that
modulate eye, lens, and corneal growth in the mouse. For example, compare
eye and lens weights in strain 129/J with that of C57L/J. Both have lenses
that weigh approximately 6.0 mg, but the total eye weight of 129/J is 12%
less. The immediate question is whether there are refractive and
functional differences: is one strain emmetropic and the other not? Does
corneal power compensate for differences in lens and eye dimension? When
does this difference first develop? While we do not have answers to these
questions, we have screened a sufficient number of strains to identify
those outliers that are candidates for more detailed developmental and
genetic analysis.
The mouse as a myopia model
Over the past several decades, several powerful animals models have
been developed and exploited to study environmental, functional, and
biochemical processes that contribute to myopia.27–35
From a functional point of view, the disadvantages of the mouse–a small
nocturnal species without any significant central retinal
specialization—are obvious. But the mouse offers a complementary and
highly efficient animal model that can be used to explore the genetic and
molecular basis of the growth of major parts of the eye. 16
For this particular purpose the mouse is currently unrivaled.
Mapping eye growth genes
In a recent study we have demonstrated that eye growth in mice is
strongly modulated by two gene loci—one located on the proximal end of
chromosome 5, the second near the major histocompatibility complex on
chromosome 17.17
Mapping these genes that modulate eye growth is only the first step in our
analysis. The second step is to identify and verify candidate genes. The
chromosome 5 locus, Eye1, is tightly linked to (and could be
identical to) the hepatic growth factor gene, a mitogen that is expressed
in the sclera, choroid, and retina during development. Once key genes have
been cloned, it will be possible to explore molecular networks in detail
and to determine if and how such genes modulate eye growth in humans.
The power of strain comparisons
We have characterized only a few ocular traits in 50 strains. There are
numerous other interesting parameters, particularly axial measurements,
refractive powers, intraocular pressures (IOP), and functional measures of
vision that one might want to obtain.36 Since
all of these mice are inbred and commercially available, it is feasible to
add to an expanding database on the eyes of mice—to refine and define
mouse models. For example, John and colleagues37,38
have recently demonstrated that there are significant differences in
intraocular pressure among five inbred strains of mice that we have
quantified—from 7.7 mm Hg in BALB/cJ to 13.7 mm Hg in C3H/HeJ. It is
therefore possible to assess whether differences in eye weight are
associated with the IOP. The IOP dataset is still too small for reliable
statistical inference, but this work now indicates that there may in fact
be an inverse relation between variables (r = –0.59, n of
5).
One of the more important findings of this study is the relative
weak dependence between the growth of the lens and the posterior segment
(assessed either as the retinal area or as the weight of the non-lenticular
part of the eye). The wide range of ratios of lens weight and eye weight
suggests that the mean refractive status of strains may be highly variable
(Fig. 3). It should be possible to isolate strains of mice that are
hyperopic and myopic and it should be possible to tease apart genetic and
developmental processes that separately control the growth of major
components of the eye.
Growth of the eye in adult mice
The continuous growth of the adult eye and lens was an surprising
finding. The adaptive significance, if any, of this process in unknown,
and in this respect, eye growth in mouse and humans appear to differ.19,20,39
The size of the human eye does not normally increase
steadily as a function of age much, if any, beyond sexual maturity. In
fact, between 10- and 18-years-of-age, the axial length of the human eye
typically grows by merely 0.5 mm.19 A slight
flattening of the lens normally counterbalances this growth.
Unlike the weight of the whole eye, the weight of the lens does
increase a surprising amount with age in humans. Harding and colleagues
26 report that average lens weights taken from a
large sample of British subjects (n = 207) increased from 150–170
mg during the teens to 210–230 mg by 65 years-of-age. This is equivalent
to a gain of 1.2 mg per year.
The lens of humans is a relatively small part of total eye weight
(roughly 3%), but in mice the lens makes up 30% of total eye weight. Thus
a 3.6-mg gain in lens weight in the mouse between 40 and 400 days has far
greater effect on total eye weight than does a 60-mg increase in lens
weight in a human between 16 and 65 years of age. This could explain some
of the significant difference between mouse and human.
From an experimental point of view—and from the point-of-view of
developing new genetic models to study eye growth—the log-linear growth of
the eye and lens of mice is of practical interest. The rate of eye growth
in mice can potentially be changed in either direction by experimental or
genetic manipulations.
Heritability
Eye weight among normal adult mice varies from 14 to 24 mg, and under
carefully controlled laboratory conditions approximately one-third of this
variation is generated by genetic factors. Estimates of heritability for
lens weight and retinal area are of the same magnitude. Since the mice
that we studied were born and raised in a tightly controlled environment,
estimates of genetic control that we have generated, while typical of lab
mice, will not be representative of wild populations or of humans.
However, our sample did include a wide range of ages, males and females
taken from different litters and different mothers within strains. In any
case, levels of heritability of all three ocular traits are sufficiently
high—between 25% and 40%–to justify searching for individual genes that
contribute to genetic variation in eye, lens, and retinal growth in mice.15–17,23
A substantial number of studies have assessed the heritability of
variation in the size, shape, and refractive status of the human eye.13,14,40–45
Estimates of heritability are difficult to assess primarily because of
marked changes in environment and the highly variable reading and viewing
habits of human, 13,46 but the majority of
estimates range from 25% to 50%.44,47 Higher
values have been inferred from some twin samples,48,49
but significantly lower values have been computed after compensation for
shared familial patterns of education and near-work. In a particularly
careful analysis that compensated well for environmental factors, Bear et
al.46 estimated that the heritability of myopia
was between 10% and 30%.
Emmetropia in rodents?
Although mice and rats are frequently reported to be moderately to
highly hyperopic, the technical difficulties and biases of retinoscopic
assessment of such small eyes make a significant contribution to apparent
refractive errors. 50–53 We assume that wild
populations of mice are free of significant mean refractive error, but
whether this is true of highly inbred laboratory strains that are not
subject to normal patterns of selection is unknown. It is certainly
interesting that correlations between lens weight and the weight of the
remainder of the eye are so weak. On the one hand, it is possible that the
lack of a tight correlation reflects the highly variable refractive state
of different strains and individuals. Perhaps only a small fraction of
mice are emmetropic. On the other hand, it is not inconceivable that
differences in corneal curvature or the refractive index and shape of the
lens compensate for differences in axial length and lens weight to insure
emmetropia.
The analysis of mice with retinal degeneration is useful in
exploring this issue of the role of normal vision in eye growth. In these
rd1 mice there is minimal adaptive utility to maintaining
emmetropia and eye growth and lens growth are presumably uncoupled
functionally. Since the correlation between lens weight and eye minus
lens weight is 0.54 in rd mice—an insignificant drop from the
correlation in mice with intact photoreceptors (0.59)–it seems unlikely to
us that most inbred laboratory mice are emmetropic (see Fig. 3). This may
explain why anatomical estimates of peak acuity in inbred mice exceed
behavioral estimates by a factor of nearly three (1.4 vs. 0.5
cycles/degree).54
Genetics of eye development
We know a great deal about gene mutations that disturb the development
of the eye, resulting in anophthalmias, aplasias, colobomas, cataracts,
photoreceptor degeneration, glaucomas, etc.55–64.
In contrast, we know almost nothing about genes that are responsible for
the far more pervasive but more modest variation in eye size and structure
among normal individuals.16,23 An obvious
question is whether the normal variation in eye size and the
susceptibility to myopia in human populations is produced by normal
allelic variants at gene loci that are already known to influence eye
development. For example, might subtle change in amino acids of the
Chx10 or Pax6 gene products be responsible for some of the
differences?61,65
While our own work on this topic is at an early stage, we now have
some indication that the types of genes that control quantitative
variation in eye traits—so called, quantitative trait loci—may indeed
correspond to genes already known to have key roles in eye development.
The tantalizing linkage between Eye1 and the hepatic growth factor
on chromosome 5 is one example.15 The linkage
between Nnc1 and thyroid hormone alpha receptor on chromosome 11 is
another example.23,66 In the next few year it
may be possible to determine the actual gene sequences responsible for
relatively subtle differences in eye growth in mice. This should
ultimately make it possible to separately modulate the rates of lens and
corneal growth and the expansion of the posterior segment of the eye. As
we learn more about molecular pathways that regulate growth of the eye, it
should be feasible to develop novel therapeutic methods to ensure normal
eye growth and vision in humans.
ACKNOWLEDGMENTS
This research was supported by NIH grant EY06627 from the National Eye
Institute to RW. We thank Dr. Linda Siracusa for providing us with
additional BXH strains. We thank Alexander Williams for developing WWW
databases available at
nervenet.org.
REFERENCES
- Altman PL, Dittmer DS. Growth including reproduction and
morphological development. Washington, DC: Fed Amer Soc Exp Biol. 1962.
- Walls GL. The vertebrate eye and its adaptive radiation. Cranbrook
Institute of Science, Bulletin N. 19. MI: Bloomfield Hills, 1942.
- Dawkins R. Climbing Mount Improbable. London: WW Norton, 1996.
- Chase J. The role of vision in echolocatiing bats. Ph.D. thesis,
Indiana University, 1972.
- Lythgoe JN. The ecology of vision. Oxford: Clarendon Press, 1979.
- Roff DA. Evolutionary quantitative genetics. New York: Chapman &
Hall, 1997.
- Lynch M, Walsh B. Genetics and analysis of quantitative traits.
Sunderland, MA: Sinauer, 1998.
- Lande R. Quantitative genetic analysis of multivariate evolution,
applied to brain:body size allometry. Evolution 1979;33:234–251.
- Wilkens H. Genetic interpretation of regressive evolutionary
processes: Studies on hybrid eyes of two Astyanax cave populations (Characidae,
Pisces). Evolution 1971;25:530–544.
- Land MF. Optics and vision in invertebrates. In: Handbook of sensory
physiology VII/6B (Aurtrum H, ed). Berlin: Springer, 1980:471–592.
- Hiller-Adams P, Case JF. Eye size of pelagic crustaceans as a
function of habitat depth and possession of photophores. Vis Res
1988;28:667–680.
- Steiger A. Die Entstehung der Sphärischen Refraktionen des
Menschlichen Auges. Berlin: Karger,1918.
- Zadnik K, Satariano WA, Mutti DO, Sholtz RI, Adams AJ. The effect of
parental history of myopia on children's eye size. JAMA
1994;271:1323–1327.
- Ashton GC. Segregation analysis of ocular refraction and myopia. Hum
Hered 1985;35:232–239.
- Zhou G, Williams RW. Mapping genes that control variation in eye
weight, retinal area, and retinal cell density. Soc Neurosci Abst
1997;23:864.
- Williams RW, Strom RC, Zhou G, Yan Z. Genetic dissection of retinal
development. Semin Cell Dev Biol 1998;9:249–255.
- Zhou G, Williams RW. Eye1 and Eye2: Gene loci that
modulate eye size, lens weight, and retinal area in mouse. Invest
Ophthalmol Vis Sci 1999; 40:817–825.
- Williams RW, Zhou G. Genetic control of eye size: A novel
quantitative genetic approach. Invest Ophthalmol Vis Sci [Suppl}
1999;40:XXX.
- Fledelius HC. Ophthalmic changes from age of 10 to 18 years. A
longitudinal study of sequels to low birth weight. IV. Ultrasound
oculometry of vitreous and axial length. Acta Ophthalmol
1982;60:403–411.
- Scammon RE and Armstrong EL. On the growth of the human eyeball and
optic nerve. J Comp Neurol 1925;38:165–219.
- Sidman RW, Green MC. Retinal degeneration in the mouse. Location of
the rd locus in linkage group XVII. J Hered 1965;56:23–29.
- Williams RW, Strom RC, Rice DS, Goldowitz D. Genetic and
environmental control of variation in retinal ganglion cell number in
mice. J Neurosci 1996;16:7193–7205.
- Williams RW, Strom RC, Goldowitz D. Natural variation in neuron
number in mice is linked to a major quantitative trait locus on Chr 11.
J Neurosci 1998;18:138–146.
- Williams RW. The human retina has a cone-enriched rim. Vis Neurosci
1991;6:403–406.
- Hegmann JP, Possidente B. Estimating genetic correlations from
inbred strains. Behav Genet 1981;11:103–114.
- Harding JJ, Rixon KC, Marriott FHC. Men have heavier lenses than
women of the same age. Exp Eye Res 1977; 25: 651.
- Young FA. The effect of restricted visual space on the primate eye.
Invest Ophthalmol Vis Sci 1963;2:571–577.
- Sherman SM, Norton T. Myopia in the lid-sutured free shrew (Tupaia
glis). Brain Res 1977;124:154–157.
- Wiesel TN, Raviola E. Myopia and eye enlargement after neonatal lid
fusion in monkeys. Nature 1977;266:66–68.
- Wallman J, Turkel J, Trachtman J. Extreme myopia produced by modest
change in early visual experience. Science 1978;201:1249–1251.
- Fernald RD, Wright SE. Growth of the visual system in the African
cichlid fish Haplochromis burtoni. Accommodation. Vision Res
1985;25:163–170.
- Wildsoet CF, Pettigrew JD. Kainic acid-induced eye enlargement in
chickens: differential effects on anterior and posterior segments.
Invest Ophthalmol Vis Sci 1988;29:311–319.
- Stone RA, Laties AM, Raviola E, Wiesel TN. Increase in retinal
vasoactive intestinal polypeptide after eyelid fusion in primates. Proc
Natl Acad Sci USA 1988;85:257–260.
- Selther RLP, Stell WK. The effect of VIP on development of form
deprivation myopia in the chick: a pharmacological and
immunocytochemical study. Vis Res 1995;35:1265–1270.
- Hung LF, Crawford MLJ, Smith EL. Spectacle lenses alter eye growth
and the refractive status of young monkeys. Nature Med 1995;1:761–765.
- Fuller JL, Wimer RE. Neural, sensory, and motor functions. In:
Biology of the laboratory mouse, 2nd ed (Green EL, ed) New York: Dover
Pub,1966:609–628.
- John SWM, Hagaman JR, MacTaggart TE, Peng, L, Smithes O. Intraocular
pressure in inbred mouse strains. Invest Ophthamol Vis Sci
1997;38:249–253.
- John SWM, Smith RS, Savinova OV, Hawes NL, Chang B, Turnbull D,
Davisson M, Roderick TH, Herkenlively JR. Essential iris atrophy,
pigment dispersion, and glaucoma in DBA/2J mice. Invest Ophthamol Vis
Sci 1998;39:951–962.
- Fledelius HC, Christensen AC. Reappraisal of the human ocular growth
curve in fetal life, infancy, and early childhood. Brit J. Ophthalmol
1996;80:918–921.
- Donders FC. On the anomalies of accommodation and refraction of the
eye. London: New Syndenham Society,1864.
- Holm E. Myopia from the point of view of heredity. Acat Opthalmol (Copenh)
1926;3:335–347.
- Wold KC. Hereditary myopia. Arch Ophthalmol 1949;42:225–237.
- Furusho T. Studies on the genetic mechanism of short-sightedness.
Jap J Ophthalmol 1957;1:185–190.
- Sorsby A, Leary GA, Fraser GR. Family studies on ocular refraction
and its components. J Med Genet 1966;3:269–273
- Basu SK, Jindal A. Genetic aspects of myopia among the Shia Muslim
Dawoodi Bohras of Udaipur, Rajsthan. Hum Hered 1983;31:199–200.
- Bear JC, Richler A, Burke G. Nearwork and familial resemblances in
ocular refraction: A population study in Newfoundland. Clinical Genetics
1981;19:462–472
- Teikari JM, O'Donnell J, Kaprio J, Koskenvuo M. Impact of heredity
in myopia. Hum Hered 1991;4:151–156.
- Karlsson JL. Concordance rates for myopia in twins. Clin Genet
1974;6:142–146.
- Karlsson JL. Evidence for recessive inheritance of myopia. Clin
Genet 1975;7:197–202.
- Glickstein M, Millodot M. Retinoscopy and eye size. Science
1970;168:605–606.
- Hughes A. A schematic eye for the rat. Vision Res 1979;19:569–588.
- Murphy CJ, Howland HC. The optics of comparative ophthalmoscopy.
Vision Res 1987;27:599–607.
- Mutti DO, Ver Hoeve JN, Zadnik K, Murphy CJ. The artifact of
retinoscopy revisited: a comparion of refractive error measured by
retinoscopy and VEP in the rat. Optom Vis Sci 1997;74:483–488.
- Dräger UC, Olsen JF. Ganglion cell distribution in the retina of the
mouse. Invest Ophthalmol 1981;20:285–293.
- Packer SO. The eye and skeletal effects of two mutant alleles at the
microophthalmia locus of Mus musculus. J. Exp. Zool.
1967;1;21–45.
- Rice DS, Williams RW, Goldowitz D. Genetic control of retinal
projections in inbred strains of albino mice. J Comp Neurol 1995;354:
459–469.
- Rice DS, Williams RW, Harris B, Bailey PW, Davisson MT, Goldowitz D.
Mapping the Bst mutation on mouse chromosome 16: a model for
human optic atrophy. Mamm Genome 1995;6:546–548.
- Sicinski P, Donaher JL, Parker SB, Li T, Fazeli A, Gardner H, Haslam
SZ, Bronson RT, Elledge SJ, Weinberg RA. Cyclin D1 provides a link
between development and oncogenesis in the retina and breast. Cell
1995;82:621–630.
- Linden R, Pinto LH. Developmental genetics of the retina: evidence
that the pearl mutation in the mouse affects the time course of natural
cell death in the ganglion cell layer. Exp Brain Res 1985;60:79–86.
- Connell G, Bascom R, Molday L, Reid D, McInnes RR, Molday RS.
Photoreceptor peripherin is the normal product of the gene responsible
for retinal degeneration in the rds mouse. Proc Natl Acad Sci USA
1991;88:723–726.
- Burmeister M, Novak J, Liang MY, Basu S, Ploder L, Hawes NL, Vidgen
D, Hoover F, Goldman D, Kalnins VI, Roderick TH, Taylor BA, Hankin MH,
McInnes RR. Ocular retardation mouse caused by Chx10 homeobox
null allele: impaired retinal progenitor proliferation and bipolar cell
differentiation. Nat Genet 1996;12, 376–384.
- Cepko CL, Austin CP, Yang X, Alexiades M, Ezzeddine D. Cell fate
determination in the vertebrate retina. Proc Natl Acad Sci USA
1996;93:589–595.
- Freund C, Horsford DJ, McInnes RR. Transcription factor genes and
the developing eye: a genetic perspective. Hum Mol Gen 1996;5:1471–1488.
- Stone EM, Fingert JH, Alward WLM, Nguyer TD, Polansky JR, Sunden SLF,
Nishimura D, Clark AF, Nystuen A, Nicheols BE, Mackey DA, Ritch R,
Kalenak JW, Craven ER, Sheffield VC. Identification of a gene that
causes primary open angle glaucoma. Science 1997;275:668–670.
- Callaerts P, Halder G, Gehring WJ. Pax-6 in development and
evolution. Annu Rev Neurosci 1994;20:483–532.
- Strom RC, Williams RW. Cell production and cell death in the
generation of variation in neuron number. J Neurosci 1998;18:9948–9953.

Related Links of Interest:
The Retinal Information Network
Since 24 March 99
|
|
|

 Publications
Publications



