 |
| |||||
|
| ||||||||
|
| ||||||||
Home  Publications Publications |
|
|
Note to the Reader This is a revised edition of a paper published in The Journal of Neuroscience. The data described in this unpublished manuscript were generated through 1995. More recent data and corrections are available from the Neurogenetics server. The number of cases considered in this web publication is much greater than the print publication. Journal of Neuroscience 16: 719–7205
Print Friendly Contents Material and Methods
How much of the often remarkable variation in neuron number within a species is generated by genetic differences, and how much is generated by environmental or developmental factors? We address this problem for a single population of neurons in the mouse central nervous system. Retinal ganglion cells of inbred, outbred, hybrid, and wild strains were studied using electron microscopic and quantitative genetic methods. Numbers of ganglion cells range from 32,000 to 87,000. The distribution of all cases (n = 451) is close to normal and has mean of 60,000 and a standard deviation of 8,000. Male and female averages are matched to within 1%. There is no loss of ganglion cells with age over a range from 21 to 765 days of age (r = - 0.031). Genetic factors predominate in the control of ganglion cell number. Estimates of additive gene effects (narrow-sense heritability) range from 70% to 85%. Estimates of total genetic determination (broad-sense heritability) reach close to 90%. In contrast to individual counts, the averages of 40 homozygous strains have a striking bimodal distribution, with peaks at 55,000 and 63,000 cells. This suggests that single quantitative trait loci control much of the variation among mice. The coefficient of variation within isogenic strains averages about 4.5%. Most of this non-genetic variation in neuron number within groups of isogenic mice appears to be produced by developmental noise rather than by conventional environmental factors.
IntroductionThre is a great deal of variation in the size of neuron populations among individuals within a species. For example, the number of giant interneurons in the spinal cord of sea lampreys ranges from 12 to 22 (Selzer, 1979). At the other extreme, the number of neurons in the lateral geniculate nucleus of rhesus macaque monkeys ranges from 1.0 to 1.8 million (Williams and Rakic, 1988a; Ahmad and Spear, 1993). The adaptive significance of this wide variation has not yet been explored in detail (Williams and Herrup, 1988), but there is a rough relationship between neuron number and an animal's behavioral capacity (Wimer and Wimer, 1985; Purves, 1988; Lipp et al., 1989; Crusio et al., 1989a,b; Legendre et al., 1994; Stevens, 1994; Tejedor et al., 1995). Variation in the size of cell populations is therefore likely to be an important target of natural selection (Williams et al., 1993). But variation can be traced to many causes, and a key problem now is estimating their relative importance. How much of the variance in single neuron populations is due to heritable gene effects? How much is generated by the environment, and how much is generated by random fluctuations in cell cycle kinetics, cell commitment, and cell death? To rephrase this in a complementary way—how precisely does the genome, in concert with an intricate array of developmental processes, specify the size of cell populations? To partition variation in neuron number we have used an efficient electron microscopic method to count retinal ganglion cells. These cells are the sole projection neurons of the vertebrate retina (Rodieck and Brening, 1983), and a census of the entire population can be obtained by counting axons in a single cross-section of the optic nerve (Chalupa et al., 1984; Williams et al., 1986; Lia et al., 1986; Rice et al., 1995a). Data were collected from a variety of mice, including:
The results provide answers to several questions. We now have a good
idea of how precisely a discrete population of neurons can be regulated
when genetic differences are eliminated and when environmental
perturbations are minimized. We know the relative importance of genes and
the environment in controlling ganglion cell numbers. We have also
generated estimates of heritability that can be used to predict the
effects of selection for or against high or low cell number. Finally, this
work sets the stage to explore the genetic and developmental mechanisms
that control natural variation in neuron number in the vertebrate CNS.
Materials and MethodsTissue was taken from 451 mice belonging to 59 different strains or types (Figure 1). Most animals were shipped directly from the Jackson Laboratory (Bar Harbor, Maine). The mix of sexes among strains varied, but the ratio across all strains was close to 1:1. The age of mice ranged from 21 to 765 days. No systematic attempt was made to ensure that the average age or sex ratio among strains was matched. While at the Jackson Laboratory most animals were fed a 6% fat NIH31 diet. With three exceptions, all BXD recombinant inbred strains were fed a high fish oil diet (Wayne Lab Tech). Strains BXD13, BXD20, and BXD31 were fed a 9% fat diet (modified NIH 911A). While housed at the University of Tennessee mice were fed a 5% fat Agway Prolab 3000 rat and mouse chow. Colonies were maintained at 20-24 °C on a 14/10 h light-dark cycle.
Standard inbred strains. Standard inbred laboratory strains of mice (Fig. 1, middle group) are derived from domesticated hybrids generated from crosses between Mus musculus domesticus (also known as M. domesticus) and M. musculus molossinus (Silver, 1995). All of the standard strains that we studied have been inbred by successive sibling matings for more than 80 generations (Festing, 1993). Animals are therefore homozygous at essentially all loci. C57BL/6Ax1 is a non-standard nomenclature we have introduced (see Results) to designate animals obtained from the Jackson Laboratory Annex 1 colony. The particular strains that we studied were for the most part selected without regard to CNS or ocular characteristics. TgN(Hbb-b1)/LoGo (abbreviated TgHBB) is a transgenic strain derived from a cross between SJL/J and C57BL/6J. TgHBB was inbred for 10 to 15 generation (C. Lo, personal communication), but has been maintained for several years by quasi-random mating. We have not used this strain in calculating heritabilities. We have also not used a partially inbred strain, B6C3/FeJ, in these calculations. Wild strains. We studied four species of mice: 1) M. musculus, the common house mouse, a wide-ranging and highly adaptable commensal species from which laboratory mice are derived (Bronson, 1984); 2) M. spretus (SPRET/Ei), a short-tailed field mouse distributed around the western Mediterranean; 3) M. spicilegus (PANCEVO/Ei), a colonial mound-building species from the Balkans and Ukraine; and 4) M. caroli (CARL/ChGo), a small tropical East Asian species (Fig. 1, bottom group, Table 2). We also studied four subspecies of M. musculus: 1) M. m. castaneus (CAST/Ei and CASA/Rk), a South East Asian subspecies; 2) M. m. musculus (CZECHII/Ei), the commensal Eastern European and Asiatic mouse; 3) M. m. molossinus (MOLD/Rk), a Japanese hybrid subspecies; and 4) M. m. domesticus (WSB/Ei), the commensal and very widely dispersed subspecies of Western Europe and the Americas (Fig. 1, bottom group, Table 2). Seven of these wild strains have been inbred for more than 16 generations at the Jackson Laboratory. The exception is CARL/ChGo—an outbred wild sample of Mus caroli maintained since the middle 1970s as a colony of 5-10 breeding pairs with specific avoidance of sib mating (V. Chapman, personal communication). The evolutionary relations and ecological characteristics of these species are reviewed briefly in Bonhomme and Guénet (1989), Nowak (1991), and Bonhomme (1992). Genetically heterogeneous mice. Several types of mice included in this study are genetically heterogeneous. The first is referred to as CD-1 or ICR (Hsp:ICR). This strain has been bred for high fecundity and fitness (Eaton, 1980), and is maintained by random non-sib matings at Harlan Sprague Dawley Inc. (Indianapolis, IN). The strain is derived from non-inbred Swiss albinos originally designated HaM/ICR (Hauschka and Mirand 1973). The second is CARL/ChGo, described above (Wild strains). The third and most heterogeneous group is made up of the F2 progeny of a cross between BALB/cJ and CAST/Ei. These progeny are referred to as BCF2 (Fig. 1, Test cross). BCBN2 and BCCN2 are the backcross progeny generated by crossing BCF1 females to BALB/cJ and CAST/Ei males, respectively. Isogenic F1 hybrids. We studied five sets of isogenic F1 hybrids (Fig. 1). Four of these were hybrids between a BALB/cJ parent and either an A/J, C57BL/6J, C57BL/6JAx1, or CAST/Ei parent. They are referred to as CB6F1/J (a BALB/cJ female crossed to a C57BL/6J male), B6AxCF1 (the cross between a C57BL/6JAx1 mother and a BALB/c father), CAF1 (BALB/cJ female by A/J male), and BCF1 (BALB/c female by CAST/Ei male). We also examined the PLSJF1 progeny of a cross between PL/J and SJL/J. The CAF1, CB6F1, and PLSJF1 were obtained from Jackson Laboratory. The B6AxCF1 and BCF1 progeny were generated in our colony from animals obtained from the Jackson Laboratory. In this paper we treat both these F1 hybrids and the fully inbred strains as isogenic. Formally, only animals of the same type and sex are isogenic. BXD recombinant inbred strains. We studied 26 of the BXD recombinant inbred strains (Fig. 1, top group). These strains were generated by inbreeding the hybrid progeny of matings between C57BL/6J and DBA/2J mice. The genome of each BXD strain is an isogenic mosaic of C57BL/6J and DBA/2J chromosomal segments (Bailey, 1981; Taylor, 1989). Mutants. Several strains carry mutations that affect the retina. Five strains that we studied (C3H/HeJ, CD-1, PL/J, SJL/J, and MOLD/Rk) carry the retinal degeneration allele, rd, at the beta-phosphodiesterase locus. These strains lose virtually all photoreceptors by two months of age. With the exception of MOLD/Rk, all rd strains have normal nerves, and several have high ganglion cell populations. Eight of the strains we used are albinos and have a reduced proportion of retinal ganglion cells with uncrossed projections (A/J, AKR/J, BALB/cBy, BALB/cJ, CD-1, 129/J, NZW/LacJ, SJL/J, see Rice et al., 1995a). We have not noted any correlation between pigmentation and total ganglion cell number. Fixation and processing of tissue. Mice were anesthetized with an injection of Avertin (0.5-0.8 ml ip) and were perfused transcardially with 0.9% saline followed by fixative using a peristaltic pump. Approximately 15 ml of 1.25% glutaraldehyde and 1.0% paraformaldehyde in 0.1 M phosphate buffer was injected for 2-4 min. An additional 10 ml of double-strength fixative (2.5% glutaraldehyde and 2.0% paraformaldehyde in the same buffer) was injected for 1-2 min at an increased flow rate. The head was removed and placed in fixative overnight at 4 °C and placed in 0.1 M phosphate buffer the next morning. Optic nerves were dissected and were subsequently osmicated and embedded in Spurr's resin. For most cases, the brains, including olfactory bulb, were dissected free, trimmed just behind the cerebellum, and weighed. Thin sections of either nerve were placed on Formvar-coated slot grids and were stained with uranyl acetate and lead citrate. The nerves were examined and photographed on a JEOL EX2000II microscope using a systematic unstratified sampling protocol (Fig. 2A, Deming, 1950). An important variable determining count precision is the accuracy with which image magnification is measured (Fig. 2B,D). Magnification was calibrated by photographing a grid replica (EMS, Ft. Washington PA, # 80051, 2160 lines/mm) at the conclusion of every photography session. The procedure was performed in the following sequence:
The overall image quality of each set of micrographs was scored using a four point scale. The correlation between these scores and the within-strain standardized z score of the count was used to assess the sensitivity of estimates to fixation and image quality. After discarding about 25 cases that scored in the worst image and fixation category, the correlation was close to zero (r= 0.07). The average z score for samples ranked adequate was -0.246 z, whereas that for samples ranked excellent was +0.034 z. Given the small size of the effect, no compensation was applied.
Legend to Figure 2. A set of four marked contract prints (1:1 reproduction) of negatives used to generate estimates of ganglion cell number. A and B are matched low power transmission electron micrographs of the ultrathin section (A) and the calibration grid (B). The series of white spots in A are regions bleached during the high magnification sampling. The outline of the nerve was traced on the negative under a dissecting microscope. The boundary was drawn across the outer rank of axons, even if that involved an occasional intrusion into the nerve. The area of the nerve was computed by tracing this boundary using a calibrated digitizing tablet two or more times (see faint numbers, upper left in A). The asterisk in A marks the site illustrated at higher magnification in C. Two sites marked by arrows on the calibration negative (B) have been measured. The upper site (inset) is illustrated at higher magnification. A series of 41 marks, spanning 80 grid units, were made with a microscalpel. The separation between endpoints was measured under a dissecting microscope with a digital caliber accurate to 10 µm. Distances on all calibration negatives were measured two or four times in the two orthogonal axes of the grid. C is one of the sample negatives that illustrates the counting frame and the axons that were counted. The three faintly circled axons are unmyelinated. D is the high magnification calibration grid used to compute the sample area. Grid dimensions are 0.463 x 0.463 µm. If one calculates the axon population just from these four micrographs, the estimate should be close to 81,500. However the average axon count for the 22 sample micrographs was 40.5 ± 9.07, giving an estimate of 68,669 ± 3,361. This case was replicated independently, and the other estimate from a different thin section was 68,154 ± 3,329. The final estimate was 68,409 ± 2,365 (variance weighted average). The standard deviation and its derivates such as the standard error of the mean and the coefficient of variation are seriously biased for small sample size (Sokol and Rohlf, 1981). For example, a standard deviation estimated from a sample of two cases will on average underestimate the population standard deviation by 25%. Because the number of cases we studied per group varied from 4 to more than 20, we needed to correct for this bias. Gurland and Tripathi (1971) provide the corrections for this bias. The factors are reproduced below for sample sizes of between 2 and 39. Note that variance estimates are not subject to this bias.
*The standard deviation should be multiplied by the correction factor. Do not over-correct by subsequently using these factors on the standard error of the coefficient of variation. Estimates of genetic determination. We used complementary methods to calculate heritability. The additive genetic component from inbred strain data was computed using the method of Hegmann and Possidente (1981). The confidence intervals of these estimates were computed using a jackknife procedure (Mosteller and Tukey, 1977, p. 135). The uncertainty of the strength of additive gene effects were assessed directly by counting independent sets of inbred strains. One set consisted of 17 standard strains (Fig. 1, middle panel); the other set consisted of 23 recombinant inbred strains (Fig. 1, upper panel). Gene dominance, heterosis, and inbreeding depression were estimated from 1) F1 heterozygotes, 2) Mendelian test cross progeny, and 3) by comparing inbred and outbred populations (Falconer, 1989). Estimates of broad-sense heritability, or total genetic determination, were computed by comparing levels of variance in outbred and isogenic groups (Vogel and Motulsky, 1986; Crusio, 1992; Wahlsten, 1992), both before and after correcting for technical variance. It is worth emphasizing that most quantitative genetic procedures and heritability estimates in particular, are not designed to address modes of gene action or specific developmental processes. These methods provide global insight on the mean effects of genes on phenotypes within specific populations and under specific environmental conditions (Cheverud, 1984, 1990). Reliability and accuracy of estimates. To directly assess total
technical variance, 116 nerves were counted two or more times. All of
these replicate counts are listed in table 1 within parentheses. Usually
an adjacent thin section was photographed and counted several months after
the original sample. Interobserver sources of variance were assessed in a
subset of 28 replicates in which photography, calibration, and counting
were done by different individuals. The test-retest reliability
coefficient r(TX) across all replicates was approximately 0.77 (Snedecor
and Cochran, 1980; Wahlsten, 1992). The mean absolute difference between
pairs of estimates was 2,415 and the standard deviation between these
pairs averaged 3,435 (n = 129 paired comparisons). The technical
coefficient of variation (CV) for individual samples of about 25
micrographs averaged 5.70 +/- 0.1% SE. The effective sampling error over
all cases was 4.65%. For the interobserver replicates the CV was 6.6%. The
cumulative average technical variance, including all replicates for all
451 cases, averaged 5.28%. The relationship was used to obtain a more accurate estimate of the average environmental variation for groups of isogenic strains. We assume that there is no covariation between technical and strain variation. Replicated cases were not chosen randomly, but usually represented the highest and lowest cases in each strain (Table 1). This non-random selection could have inflated estimates of technical error. However, a comparison with cases that were selected randomly for replication demonstrate that this bias is negligible. Confirmation of count accuracy. Counts of peroxidase-labeled ganglion cells in 17 cases (Rice et al. 1995a for methods) confirm the accuracy of the electron microscopic method used to estimate ganglion cell number. The average axon count for these cases was 57,474 ± 1,766 (standard error of the mean, SE), whereas the estimates based on counting peroxidase labeled ganglion cell bodies in these same cases averaged 55,850 ± 2,007; an insignificant difference.
*Updated or new cases since publication in 1996.
ResultsThe Results are divided into four sections. The first is a summary of data pooled across all strains analyzed with respect to age, sex, and brain weight. The second part surveys differences in cell number between strains and includes an analysis of the bimodality of strain averages. The third section summarizes variation in ganglion cell numbers within isogenic mice. The final section deals with heritability and variation in cell number among Mendelian test cross progeny.
Distribution of cell number and correlations with age, sex and brain weightDistribution of individual values. The average and standard deviation for all cases listed in table 1 is 59,692 ± 7,953 ( ± 375 SE). The distribution is unimodal and close to normal (Figure 3). We have included a wide diversity of types of mice (Fig. 1) and for this reason the distribution might have been expected to have extended tails. However, near normality extends over a range of four standard deviations. There is a small but significant deficit in the expected number of cases with populations close to the average (asterisk in Fig. 3) that gives the distribution a slightly flattened shape compared to the expected Gaussian distribution. This deviation has a straightforward explanation—we sampled many homozygous mice (Table 1), and these homozygous mice tend to have polarized phenotypes. Legend to Figure 3. Distribution of individual counts. In this stem and leaf display each case is encoded as a single digit (see Interpretation). The figure can be read as a vertical histogram with bins of 1,000 cells and bars made up of rows of digits. The bold black curve is the observed probability density calculated from the sum of 451 individual Gaussian probability functions. In contrast, the predicted Gaussian probability density (fine line and gray region) is based on the sample average and standard deviation of 59,692 ± 7,953. The median is 60,000 and the quantiles are at approximately 54,300 and 65,100. The asterisk highlights the deficit of expected cases close to the mean. Values below 40,000 and above 80,000 are enclosed within parentheses. Excluding the 23 animals that do not belong to the M. musculus complex (Fig. 1; CARL/Go, SPRET/Ei, and PANCEVO/Ei) does not alter the distribution in any significant way. Age and the ganglion cell population. The average longevity of strains of mice ranges from 300 to 850 day (Green and Witham, 1991). Our estimates were taken from animals averaging 82 days old, but with a range extending from 21 to 765 days. The youngest 66 mice—between 20 and 36 days old—had an average population of 58,542 ± 925 (SE). The oldest 54 animals—retired breeders between 180 and 765 days old—had an average population of 57,636 ± 1,128. This difference is not significant. As expected from these age averages, the correlation coefficient for the entire set of animals is very close to zero (r = - 0.03). Sex and the ganglion cell population. There are no sex differences in retinal ganglion cell number. The average population for 236 females is 59,422 ± 520 SE (average age of 87 ± 6 days), whereas that for 215 males is 59,989 ± 543 SE (average age of 76 ± 4 days). There is no evidence of sex difference within any strains. Brain weight and the ganglion cell population. We were interested in assessing whether differences in ganglion cell numbers among mice are closely associated with differences in brain weight (cf. Williams et al., 1993). The correlation between neuron number and brain weight across all cases for which both parameters were measured is 0.32 (n = 372). A stronger correlation between brain weight and the ganglion cell number emerges when strain averages are used. The correlation is 0.59 both for the set of species and subspecies listed in table 2 and for the 17 standard inbred strains listed in table 3. The correlation among the BXD strains listed in table 4 is 0.54. Collectively, this analysis indicates that as much as 30% of the variance between strains in ganglion cell number may be associated, directly or indirectly, with differences in brain weight. However, the correlation coefficient among the genetically heterogeneous BCF2 progeny (see Test cross progeny below) is 0.28, and the explained variance for this group is only 8%. Finally, the correlation within isogenic strains between these two variables is close to zero (r = 0.14 ± 0.08 SE; based on 40 within-strain correlations). This low correlation (r² = 2%) is particularly important because it indicates that environmental factors do not have significant common effects on both ganglion cell number and brain weight.
Survey of variation among species, subspecies, and strains of miceVariation among species and subspecies. We examined animals belonging to four different species of the subgenus Mus. Given the significant ecological, biogeographic, and genetic differences between these species (Nowak, 1991; Bonhomme 1992), the ganglion cell population has a comparatively narrow range extending from about 45,000 to 60,000 (Fig. 1, Tables 1, 2). We also examined several subspecies of M. musculus that are known to have contributed to the genome of the common laboratory mouse (Fig. 1, Tables 1, 2). These wild inbred M. musculus strains also have averages that range between about 45,000 and 60,000 ganglion cells. An analysis of variance demonstrates a significant difference between species and subspecies (F [7, 50] = 11.2, P < 0.001).
*Abbreviations in this and all other tables are SE: standard error of Variation among standard laboratory strains. Estimates of ganglion cell number in the 17 standard inbred strains range from 51,200 in A/J to 67,000 in C3H/HeJ (Tables 1, 3, Fig. 1, middle group). The variance between strains is also much greater than that within strains (F [16, 113] = 11.4, P < 0.001). The inbred strains are in many cases closely related by descent. Yet we find that even closely related strains have large differences in ganglion cell number (Fig. 1, Table 3). For example, strains 129/J and LP/J originated from a common ancestor in the mid-1920s but their mean populations now differ by 11,500 cells or 20% (Scheffé t = 4.75, P < 0.05 two-tailed for six comparisons). An equally large difference of 11,200 cells exists between the closely related strains, C3H/HeJ and CBA/CaJ (t = 6.22, P < 0.05). We discovered a remarkable difference of about 11,800 cells between groups of C57BL/6 mice (Table 3). The initial ten animals received from the Jackson Laboratory prior to the summer of 1994 included six standard pigmented C57BL/6J animals (4 females, 2 males) and four coisogenic c2J albinos (2 females, 2 males). These two subsets gave averages of 53,800 ± 2,000 and 52,800 ± 2,600, respectively (see Rice et al., 1995a and Table 1) that are close to the previous estimate of 56,700 ± 3,200 obtained by M.A. Williams and colleagues (1990) using similar methods. However, C57BL/6J mice obtained from the Annex 1 production colony of the Jackson Laboratory in three separate shipments in the second half of 1994 gave estimates averaging 66,100 ± 1,600 (5 females, 4 males; Table 1). This is far above the average for the first ten cases (t = 6.29, P < 0.05). More recent estimates of C57BL/6J animals obtained from a different Jackson Laboratory production colony (Annex 10) match the low number phenotype (56,026 ± 2,928, n = 6). Brain weights in the high and low groups do not differ appreciably—459 ± 5.3 mg for Annex 1 cases versus 471 ± 4.6 mg for the C57BL/6J mice. We have not identified any non-genetic factors that could have caused this difference. The difference is probably due to the fixation of a single mutation in the Annex 1 colony.
*SD and SE have been corrected using the Gurland and Tripathi (1971)
equation.
Variation among the BXD recombinant inbred strains. The BXD strains were generated by crossing C57BL/6J and DBA/2J mice (Taylor, 1978). The two parental strains have populations of 54,600 ± 900 and 63,400 ± 1,200 cells, respectively. Average neuron numbers of the 26 BXD recombinant strains extend well beyond the parental limits—from 50,900 ± 1,100 to 75,800 ± 2,200 (Tables 1, 4). The broad range is associated with a high F ratio (F [22, 119] = 16.0, P < 0.001). Two of 26 BXD strains had populations near 75,000, a level not approached in any of the other strains.
*SEs and SDs are corrected (see Materials and Methods).
Bimodality of strain averages. The average number of neurons across all 43 homozygous strains listed in Tables 3 and 4 is close to 60,000, but this value corresponds to a surprising gap in the distribution (Fig. 4). A chi-square test confirms that this distribution is not Gaussian (chi^2 [7] = 16.1, P < 0.025). A simple alternative is that the underlying population has two modes. To test this idea we computed the normalized probability densities for the set of 17 inbred strains and for the set of 23 BXD strains. This procedure involves calculating the Gaussian probability density for each strain average (see the small functions labeled C57BL/6J and DBA/2J in Fig. 4). These functions are then summed to give a cumulative probability density. In essence, a probability density is a histogram in which Gaussian functions rather than single values are tallied. The probability functions for both groups are bimodal (Fig. 4), and both are remarkably similar in shape. The main difference between the two functions is the third mode at about 75,000 in the recombinant inbred group generated by BXD5 and BXD32. Collectively, 13 of the 43 inbred strains have populations that range from about 51,000 and 56,000. They make up a low phenotype group that has a mode near 55,500. Among these 13 strains the 95% t-distribution confidence interval extends no higher than 59,000. A second, and more sharply resolved group is made up of 24 strains, all of which have means between 61,000 and 68,000. In none of these strains does the lower limit of the 95% t confidence interval extend below 58,000. Four of the BXD strains—BXD1, BXD12, BXD20, and BXD21—have intermediate cell populations between 56,500 and 60,500. Finally, two strains—BXD5 and BXD32—have averages far above the second mode and may represent a third very high cell number phenotype. The two probability densities in figure 4 can themselves be summed. The modes of this cumulative function are at 55,000 and 63,500. The low point between the two modes falls at 58,000. Legend to Figure 4. Bimodal distributions of ganglion cell numbers. The function labeled 17 inbred strains is based on data in Table 3. For each inbred strain, the Gaussian probability density of the sample mean was computed at 500 cell intervals. Values were summed and divided by 17 to obtain a normalized cumulative probability for this group. The plot labeled BXD strains was computed in the same way using data listed in Table 4 (the parental strains were excluded). The individual distributions are shown for C57BL/6J and DBA/2J—the two strains used to generated the BXD recombinant inbred strains. These strain-specific Gaussian distributions provide a sense of the contribution that single strains make to the cumulative density (values for these two small distributions have been divided by 23).
Variation within isogenic strainsThe level of variation within isogenic and non-isogenic groups. Variation in neuron number within members of isogenic groups is due to environmental and non-genetic developmental effects. We have already discounted the likelihood that sex differences or age contribute to normal variation among mice, but this still leaves room for numerous non-genetic sources of variation, including maternal care, litter size, and developmental noise (Wright, 1968, chapter 5). But the dominant source of quantitative variation within isogenic groups in this study is technical error. This technical variance had to be measured and eliminated before we could estimate the magnitude of genuine non-genetic effects. By repeating counts of 116 cases—in several cases three or even four times (Table 1, and see Material and Methods)—we determined that the standard deviation between pairs of counts from the same nerve averaged approximately 4,000 ± 400 (SE). Of this technical variance, 60-70% was due to the density with which we sampled each case (about 25 samples per nerve) and the remainder was due to calibration and measurement error. Had we sampled six adjacent thin sections from a single nerve, rather than six sections from different cases, our apparent non-genetic coefficient of variation would still have amounted to about 6.5%/ This is our average technical variance for a single estimate. The average variation within isogenic strains prior to any replication was 7.9%. We subtracted the square of the technical variance from the square of the mean total variance to obtain a more realistic estimate of non-genetic effects on the ganglion cell population (see Materials and Methods). For all of the inbred strains listed in tables 3 and 4 the corrected environmental coefficient of variation averages 4.60% ± 0.4%. Sensitivity to environmental factors is likely to vary among groups of inbred strains. The uncorrected coefficients of variation for single isogenic strains range from 3 to 10%. The average coefficient of variation for 17 standard inbred strains prior to any corrections for technical error, is 6.5% ± 0.5%. The average corrected variation of the BXD recombinant inbred strains is 5.8% ± 0.4%. Compared to these laboratory strains, the coefficient of variation for seven wild inbred strains is higher—9.7% ± 2.3%. The higher variability in wild mice is presumably due to adverse gene-environment interaction effects associated with their often poor adaptation to laboratory rearing conditions. While we have not been able to formally demonstrate a significant level of non-uniformity of variance between individual strains (Bartlett's chi-square [39] = 32.6) this is probably due to the masking effect of the fixed technical error that is included in uncorrected estimates of strain variance. [Due to the small sample number within single strains (n < 10), most strain variances cannot be effectively corrected for technical error.]
Heterosis, heritability, and test-cross resultsF1 heterosis and inbreeding depression. To assess the effects of inbreeding and the magnitude of gene dominance effects on neuron number we compared the population size and its variation between inbred strains and five sets of F1 hybrids (Table 5). Each set of hybrids is isogenic (Falconer, 1989), but because these F1s are generated by crossing very different strains, they have an especially high level of heterozygosity. The crosses included low-low, low-high, and high-high parental strain pairs. The ganglion cell population in F1 hybrids was on average somewhat higher (+1,600 cells) than the midpoint between parental strains. The largest positive deviation from the midpoint was about 5,300 cells in the F1 cross between CAST/Ei (45,000 cells) and BALB/cJ (63,400 cells). In general, the F1 results are consistent with mild heterosis and mean positive dominance at loci affecting ganglion cell number (Table 5). The relatively high population of cells in the out bred laboratory strain CD-1 (n = 68,300, Table 7) is also consistent with mild heterosis. The variation in isogenic F1s and isogenic inbred mice (wild strains excluded) do not differ significantly (Table 5 versus Tables 3 and 4; 5.8% ± 0.8% versus 6.2% ± 0.3% prior to a correction for technical variance). Thus, there is no evidence that cell number in homozygous mice is more easily perturbed by developmental or environmental factors than it is in isogenic F1 hybrids (cf. Waddington, 1957; Wayne et al., 1986; Leamy, 1992).
*Mid is the midpoint between maternal and paternal strain averages. The strength of genetic determination. A comparison of the level of variance within and between groups of inbred strains can provide an estimate of the strength of additive genetic control on neuron number (Hegmann and Possidente, 1981). Our analysis of variance demonstrates far greater variation between strains than among individuals within strains. The total variance within isogenic laboratory strains averages 15.1 (variance units are x10^6 cells^2). Estimates of this variance for two different sets of strains are close (Table 6, column Vwt). When technical error is subtracted, the average environmental variance within all isogenic inbred mice drops to 5.00 (Table 6, Vw). In comparison, variance across strains is far higher (Table 6, Vb). From these values we estimate that the narrow sense heritability, h2 is about 0.8 (Table 6). The internal errors of these estimates were computed using a jackknife procedure (Mosteller and Tukey, 1977), and the error across independent data sets is under ± 0.10. When the same estimates are made, but now without compensating for technical variance, estimates of additive genetic control range between 0.45 and 0.74. Comparable estimates of omega-squared (Wahlsten, 1992) are 0.56 for inbred and 0.70 for BXD strains. These latter estimates are lower primarily because they also do not subtract the technical error.
*Vwt = variance within strain, including technical error;
In comparison to isogenic strains, the coefficient of variation within three groups of genetically heterogeneous mice (CARL/ChGo, CD-1, and BCF2) averaged 12.8% ± 0.9%. This high value represents both a small environmental component (about 4 to 5%) and a much larger genetic component (11 to 12%). The increment in variance between isogenic strains and these outbred mice is due principally to genetic factors in a broad sense, including both dominance interactions between alleles and epistatic interactions between recombinant loci. From these values we estimated broad-sense heritability. The first estimate of 0.90 was generated by comparing the average variance in genetically heterogeneous strains (Table 7) with that in isogenic strains (Tables 3, 4, 5). The second estimate of 0.95 was generated by taking the ratio of the variance in the BCF2 progeny to the average variance within the parental strains, BALB/cJ and CAST/Ei, and their F1 hybrid, BCF1. This second value is likely to be inflated by the substantial genetic differences between the parental strains, CAST/Ei and BALB/cJ. Test cross progeny. The relative importance of additive gene effects, gene dominance, and heterosis can often be estimated by comparing intercross and backcross progeny (Falconer, 1989; Crusio, 1992). The magnitude of the additive genetic variance in F2 progeny is approximately equal to the summed variance in both backcrosses (Crusio, 1994). However, in our CAST/Ei x BALB/cJ cross the variance in the F2 progeny was substantially higher than the summed variance in the two backcrosses. This may be due to sampling error in the backcross progeny or to the disruption of epistatic complexes that stabilize neuron number in the F2s. A Mendelian test cross can be useful in estimating the approximate numbers of genes that contribute to variation (Wright, 1978; Barton and Turelli, 1989). We crossed BALB/cJ females (a high strain) to CAST/Ei males (a low strain), and then backcrossed and intercrossed these F1 progeny. If a small number of loci, each with additive effects, contribute to variation in ganglion cell number, then phenotypes of individual F2 progeny will occasionally have parental phenotypes (Falconer, 1989). In contrast, if many gene loci affect the phenotype, then the random assortment of alleles at many loci should lead to only a modest increase in variance in the F2 generation and these progeny should have intermediate phenotypes that are distributed normally. We found that variance in the BCF2 progeny was extremely high—greater even than the summed variance in both groups of backcross progeny (Table 8, Fig 4B). Many of the F2 progeny have ganglion cells populations close to, or even exceeding, the parental values (Table 1). This suggests a very small number of segregating loci. The Castle-Wright formula gives a minimal estimate of one major factor (Wright, 1978). But the relatively large number of F2 mice with very high cell numbers (overdominant phenotypes) suggests that there is at least on other locus with major effects. The unusually high variance may also be due to novel epistatic interactions introduced in the F2 generation.
*Mothers of BCCN2 and BCBN2 progeny were BCF1. Maternal factors. The observation that both the BCF1 intercross
and the BCCN2 backcross progeny have higher average cell populations than
expected suggests either that BALB/cJ alleles are dominant or that there
are positive BALB/cJ maternal effects (Wahlsten, 1983; Cowley et al.,
1989; Bulman-Fleming et al., 1991). We do note that the average population
in both F1 and F2 test cross progeny are closely
matched (Table 8). This is of interest because the mothers of the BCF1
mice were fully inbred BALB/cJ females, whereas the mothers of the F2
mice were hybrid F1 females. Both types of females had approximately the
same adult body size (25-30 gm). But in this case, reproductive heterosis
in the F1 generation is clearly not associated with F2
progeny that have higher cell number. However, these hybrid females did
produce F2 progeny with populations that ranged
over a remarkably wide range—from 45,000 to 70,000 in single litters.
Maternal effect is not a source of variation because the BCF1 mothers are
isogenic. Furthermore, the marked differences in ganglion cell numbers
among the F2 progeny are not related to
differences in brain weight (r2 = 0.08), also
indicating that maternal effect is not a significant factor in this cross.
DiscussionSynopsis. The population of retinal ganglion cells varies twofold even among closely related mice. Seventy to ninety percent of this variation can be traced to genetic differences. Sex and age differences are negligible. The coefficient of variation within groups of isogenic animals averages only 4%—a result that demonstrates that large populations of neurons in mammals can be regulated precisely. The reproducible bimodality of ganglion cell numbers among different populations of mice is an important result because it indicates that normal allelic variants at single gene loci can exert high levels of control over neuron number in the vertebrate CNS.
Environmental variation and the precision of genetic control in isogenic mammalsAn analysis of isogenic animals makes it possible to assess the
consistency with which the genome guides the generation of traits such as
neuron number. When environmental differences are minimized, the residual
variance is due to microenvironmental effects and developmental noise
(Waddington, 1957; Stent, 1981; Gavrilets and Hasting, 1994, Scheiner
1993; Cheetham et al., 1995). In a systematic analysis of the grasshopper
nervous system, Goodman (1976, 1979) found a remarkable level of variation
in neuron number both within and between isogenic groups that had been
reared in a tightly controlled environment. In one exceptional group, half
of the animals had the standard set of six ocellar interneurons whereas
the other half had seven to nine interneurons. In contrast, in a survey of
optic nerves from a set of more than 100 isogenic crustaceans, Macagno
(1980) found only a single exception to the rule of 176 axons. The
question immediately arises whether large populations of neurons in the
CNS of isogenic vertebrates are subject to high or low levels of
variation? The cellular composition of the vertebrate CNS is known to be
variable. But in the absence of an analysis of isogenic vertebrates, this
variation could be due to genetic polymorphisms rather than lax
developmental regulation.
Genetic variationGenetic differences account for most of the variation in ganglion cell
numbers among mice. Seventy to eighty-five percent of the variation is due
to the independent and additive effects of allelic variants—what is termed
narrow-sense heritability. Estimates of total genetic determination, or
broad-sense heritability—a value that includes gene dominance effects and
epistatic interactions among loci—are in the neighborhood of 90%. These
estimates neatly bracket the 80% estimate of genetic control over granule
cell number in the dentate gyrus of mice (Wimer and Wimer, 1982, 1989).
Heritability estimates such as these are based on ratios between genetic
and nongenetic variance. Consequently, minimizing environmental variance
increases measured heritability. In this study, all mice were reared in a
pathogen-free laboratory environment—a situation that eliminates numerous
sources of environmental differences, and that almost certainly increases
estimates of genetic control compared to dispersed wild populations of
mice. However, it is worth emphasizing that we included mice of a wide
range of ages, both sexes, and taken from different litters and different
mothers within strains. The environmental range that we have sampled is
appreciable and is typical of most research colonies, perhaps even stable
wild populations.
Significance of the bimodal distributionThe bimodality of strain averages is a surprising and important finding
that provides evidence that there are single polymorphic genes that have
comparatively large effects on neuron number. This conclusion is
strengthened both by the bimodality of the F2 test cross
progeny and by the large differences between three pairs of very closely
related inbred strains. A speculation based on these findings is that
variation in other neuron populations may also be controlled by relatively
small numbers of quantitative trait loci that have major effects.
Prospects for the functional and genetic analysis of natural variation in brain structureThe wide range in the ganglion cell population among mice provides
excellent material to study the functional consequences of differences in
neuron number. For example, it should be practical to test whether
differences in receptive field size and visual performance correspond to
the 50% difference in cell number between BXD28 and BXD32—two related
strains with closely matched brain weights (405 ± 8 and 429 ± 4 mg).
Exploiting the robust and large variation among inbred strains could
complement experimental studies in which dendritic diameter, receptive
field size, and contrast sensitivity have been studied with reference to
total ganglion cell number following prenatal and early postnatal lesions
(Shook et al, 1983; Kirby et al., 1985; Kirby and Chalupa, 1986; Heywod et
al., 1988). One advantage of using strains of mice is that many
individuals with well characterized phenotypes can be compared. Sampling
and technical error can be reduced to very low levels compared to
experimental manipulations (Fuller and Wimer, 1966; Lipp et al., 1989).
Strain differences also provide excellent material for developmental
studies—to determine whether variation between strains arises during cell
generation or after cell death (Linden and Pinto, 1985; Williams et al.,
1990;
Strom et al., 1995). AcknowledgementsThis research was supported by grants from the National Institutes of
Health to RW and DG and a grant from the University of Tennessee
Physicians Foundation to RW. Institutional and mouse colony support was
provide by the Center for Neuroscience at the University of Tennessee. R.
C. Strom and D. S. Rice were supported by training grant USPH SGRNS-07323.
We are indebted to Richard Cushing, Toya Kimble, and Kathy Troughton for
technical support. We thank Drs. Douglas Wahlsten, Benjamin Taylor, John
Belknap, Eric Lander, Muriel Davisson, and Richard and Cynthia Wimer for
comments and advice. Evan Williams helped count. References
Adams MD, Soares MB, Kerlavage AR, Fields C, Venter JC (1993b) Rapid cDNA sequencing (expressed sequence tags) from a directionally cloned human infant brain cDNA library. Nat Genet 4:373-380. Ahmad A, Spear PD (1993) Effects of aging on the size, density, and number of rhesus monkey lateral geniculate neurons. J Comp Neurol 334: 631-643. Agulnik S, Plass C, Traut W, Winking H (1993) Evolution of a long-range repeat family in Chromosome 1 of the genus Mus. Mamm Genome 4:704-710. Albanese A, Gozzo S, Iacopino C, Altavista MC (1985) Strain-dependent variations in the number of cholinergic neurons. Brain Res 334:380-384. Altman PL, Dittmer DS (1961) Growth, including reproduction and morphological development. Biological Handbooks. Fed Am Soc Exp Biol, Washington DC.Arnold AP, Breedlove SM (1985) Organizational and activational effects of sex steroids on brain and behavior: A reanalysis. Horm Behav 19:469-498. Bailey DW (1981) Recombinant inbred strains and bilineal congenic strains. In: The mouse in biomedical research (Foster HL, Small JD, Cox JG eds), pp 223-239. New York: Academic. Barton NH, Turelli M (1989) Evolutionary quantitative genetics: how little do we know? Ann Rev Genet 23:337-370. Belknap JK (1992) Quantitative trait loci associated with brain weight in the BXD/Ty recombinant inbred mouse strains. Brain Res Bull 29:337-344. Belknap JK, Metten P, Helms ML, O'Toole LA, Angeli-Gade S, Crabbe JC, Phillips TJ (1993) Quantitative trait loci (QTL) applications to substances of abuse: physical dependence studies with nitrous oxide and ethanol in BXD mice. Behav Genet 23:213-222. Berry RJ, Southern HN (1970) Variation in Mammalian Populations. Symp Zool Soc Lond 26:1-403. Bevington PR, Robinson DK (1992) Data reduction and error analysis for the physical sciences, 2nd ed. New York: McGraw-Hill. Bonhomme F (1992) Genetic diversity and evolution in the genus Mus. In: Techniques for the genetic analysis of brain and behavior (Goldowitz D, Wahlsten D, Wimer RE eds), pp 41-56. Amsterdam: Elsevier. Bonhomme F., Guénet JL (1989) The wild house mouse and its relatives. In: Genetic variants and strains of the laboratory mouse, 2nd ed (Lyon MF, Searle AG eds), pp 649-662. Oxford: Oxford UP. Bronson F (1984) The adaptability of the house mouse. Sci Amer 250:90-97. Bulman-Fleming B, Wahlsten D (1988) Effects of a hybrid maternal environment on brain growth and corpus callosum defects of inbred BALB/c mice: A study using ovarian grafting. Exp. Neurol. 99:636-646. Bulman-Fleming B, Wahlsten D, Lassalle JM. (1991) Hybrid vigour and maternal environment in mice. I. Body and brain growth. Behav Process 23:21-33. Berger B, Herve D, Dolphin A, Barthelemy C, Gay M, Tassin JP (1979) Genetically determined differences in noradrenergic input to the cortex. Histochemical and biochemical study in two inbred strains of mice. Neuroscience 4:877-888. Chalupa LM, Williams RW, Henderson Z (1984) Binocular interaction in the fetal cat regulates the size of the ganglion cell population. Neuroscience 12:1139-1146. Carlier M, Norsten-Bertrand M, Michard-Vanhee C (1992) Separating genetic effects from maternal environmental effects. In . Techniques for the Genetic Analysis of Brain and Behavior. Goldowitz D, Wahlsten D, Wimer, RE (eds) Elsevier, Amsterdam, pp. 111-126. Cheetham AH, Jackson JBC, Hayek LAC (1995) Quantitative genetics of Bryozoan phenotypic evolution. III. Phenotypic plasticity and the maintenance of genetic variation. Evolution 49:290-296. Cheverud JM (1990) Inheritance and the additive genetic model. Behav Brain Sci 13:124. Crabbe JC, Belknap JK, Buck KJ (1994) Genetic animal models of alcohol and drug abuse. Science 264:1715-1723. Crusio WE, Schwegler H, van Abeelen JHF (1989) Behavioral responses to novelty and structural variation of hippocampus in mice. I. Quantitative-genetic analysis of behavior in the open field. Behav Brain Res 32:75-80. Crusio WE, Schwegler H, van Abeelen JHF (1989) Behavioral responses to novelty and structural variation of hippocampus in mice. II. Multivariate genetic analysis. Behav Brain Res 32:81-88. Crusio WE (1992) Quantitative genetics. In: Techniques for the genetic analysis of brain and behavior (Goldowitz D, Wahlsten D, Wimer RE eds), pp 231-250. Amsterdam: Elsevier. Cowley DE, Pomp D, Atchley WR, Eisen EJ, Hawkins-Brown D. (1989) The impact of maternal uterine genotype on postnatal growth and adult body size in mice. Genetics 122:193-203. Deming WE (1950) Some theory of sampling. New York: Dover. Diem K, Lentner C (1975) Scientific tables. Ardsley, NY: Geigy. Dietrich WF, Miller JC, Steen RG, Merchant M, Damron D, Nahf R, Gross A, Joyce DC, Wessel M, Dredge RD, Marquis A, Stein LD, Goodman N, Page DC, Lander ES (1994) A genetic map of the 4,006 simple sequence length polymorphisms. Nat Genet 7:220-245. Durkin AS, Nierman WC, Zoghbi H, Jones C, Kozak CA, Maglott DR (1994) Chromosome assignment of human brain expressed sequence tags (ESTs) by analyzing fluorescently labeled PCR products from hybrid cell panels. Cytogenet Cell Genet 65:86-91. Eaton GJ (1980) The Icr:Ha(ICR) mouse: a current account of breeding, mutations, diseases, and mortality. Lab Ans. 14:17. Eisenberg JF (1981) The Mammalian Radiations. An Analysis of Trends in Evolution, Adaptation, and Behavior. Chicago Univ Press. Falconer DS (1989) Introduction to quantitative genetics. 3rd ed. Burnt Mill, England: Longman. Falconer DS (1963) Quantitative inheritance. In Methodology in mammalian genetics. Burdette WJ, ed. Holden-Day, Inc. San Fransisco. pp 193-216. Festing MFW (1993) Origins and characteristics of inbred strains of mice. Mouse Genome 91:393-509. Finlay BL (1992) Cell death and the creation of regional differences in neuronal numbers. J Neurobiol 23:1159-1171. Finlay BL, Darlington RB (1995) Linked regularities in the development and evolution of mammalian brains. Science 268:1578-1584. Fuller JL, Wimer RE (1966) Neural, sensory, and motor functions. In: Biology of the laboratory mouse, 2nd ed (Green EL ed) New York: Dover Pub. Gao H, Hollyfield JG (1992) Aging of the human retina: Differential loss of neurons and retinal pigment epithelial cells. Invest. Ophthalmol and Vis. Sci. 33:1-18. Gavrilets S, Hastings A (1994) A quantitative-genetic model for selection on developmental noise. Evolution 48:1478-1486. Goldschmidt R (1938) Physiological Genetics. MaGraw Hill, New York. Goodman CS (1974) Anatomy of locus ocellar interneurons: constancy and variability. J Comp Physiol 95:185-201. Goodman CS (1976) Constancy and uniqueness in a large population of small interneurons. Science 193:502-504. Goodman CS (1979) Isogenic grasshoppers: genetic variability and development of identified neurons. In: Neurogenetics: genetics approaches to the nervous system (Breakefield XO ed), pp 102-151. New York: Elsevier. Green MC, Witham BA eds (1992) Handbook on genetically standardized JAX mice. 4th ed. Bar Harbor, Maine: Jackson Laboratory. Goodman CS and Williams JLD (1976) Anatomy of the ocellar interneurons of acridid grasshoppers. II. The small interneurons. Cell Tiss Res 175:203-225. Gundersen HJG (1977) Notes on the estimation of numerical density of arbitrary profiles. The edge effect. J Microsc 111:219-223. Gundersen HJG, Bagger P, Bendtsen TF, Evans SM, Korbo L, Marcussen N, Moller A, Nielsen K, Nyengaard JR, Pakkenberg B, Sorensen FB, Vesterby A, West MJ (1988) The new stereological tools: disector, fractionator, nucleator and point sampled intercepts and their use in pathological research and diagnosis. Acta Path Microbiol Immunol Scand 96:857-881. Gurland J, Tripathi RC (1971) A simple approximation for unbiased estimation of the standard deviation. Amer Stat 25:30-32 Hahn ME, Haber SB (1978) A diallel analysis of brain and body weight in male inbred laboratory mice (Mus musculus). Behav Genet 8:251-260. Hauschka TS, Mirand EA (1973) The breeder: Ha(ICR) Swiss Mouse, a multipurpose stock selected for fecundity. In: Perspectives in cancer research and treatment (Murphy GP ed), pp 319-331. New York: Liss. Hegmann JP, Possidente B (1981) Estimating genetic correlations from inbred strains. Behav Genet 11:103-114. Herrup K (1986) Cell lineage relationships in the development of the mammalian CNS: role of cell lineage in control of cerebellar Purkinje cell number. Dev Biol 115:148-54. Herrup K, Letsou A, Diglio TJ (1984) Cell lineage relationships in the development of the mammalian CNS: the facial nerve nucleus. Dev Biol 103:329-336. Heywod CA, Silveira LC, Cowey A (1988) Contrast sensitivity in rats with increased or decreased numbers of retinal ganglion cells. Exp Brain Res 70:513-526. Johnson TE, DeFries JC, Markel PD (1992) Mapping quantitative trait loci for behavioral traits in the mouse. Behav Genet 22:635-653. Kirby MA, Chalupa LM (1986) Retinal crowding alters the morphology of alpha ganglion cells. J Comp Neurol 251:532-541. Kruska D (1987) How fast can total brain size change in mammals. J Hirnforsch 28:59-70. Lai C, Lyman RF, Long AD, Langley CH, Mackay TFC (1994) Naturally occurring variation in bristle number and DNA polymorphisms at the scabrous locus of Drosophila melanogaster. Science 266:1697-1702. Lande R (1979) Quantitative genetic analysis of multivariate evolution, applied to brain:body size allometry. Evolution 33:234-251. Lander ES, Botstein D (1989) Mapping Mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics 121:185-199. Lander ES, Schork NJ (1994) Genetic dissection of complex traits. Science 265:2037-2048. Legendre P, Lapointe FJ, Casgrain P (1994) Modeling brain evolution from behavior: a permutational regression approach. Evolution 48:1487-1499. Leamy L (1982) Morphometric studies in inbred and hybrid house mice. J Hered 73:267-272. Levinton J (1988) Genetics, paleontology, and macroevolution. Cambridge: Cambridge UP. Lia B, Williams RW, Chalupa LM (1986) Does axonal branching contribute to the overproduction of optic nerve fibers during early development of the cat's visual system? Dev Brain Res 25:296-301. Linden R, Pinto LH (1985) Developmental genetics of the retina: Evidence that the pearl mutation in the mouse affects the time course of natural cell death in the ganglion cell layer. Exp Brain Res 60:79-86. Lipp HP (1989) Non-mental aspects of encephalization: the forebrain as a playground of mammalian evolution. Hum Evol 4:45-53. Lipp HP, Schwegler H, Crusio WE, Wolfer DP, Leisinger-Trigona MC, Heimrich B, Driscoll P (1989) Using genetically-defined rodent strains for the identification of hippocampal traits relevant for two-way avoidance behavior: a non-invasive approach. Experientia 45:845-859. Macagno ER (1980) Genetic approach to invertebrate neurogenesis. Curr Top Dev Biol 15:319-345. Mackay TFC, Langley CH (1990) Molecular and phenotypic variation in the achaete-scute region of Drosophila melanogaster. Nature 348:64-66. Mosteller F, Tukey JW (1977) Data analysis and regression: a second course in statistics. Reading MA: Addison-Wesley. Mousseau TA, Roff DA (1987) Natural selection and the heritability of fitness components. Heredity 69:181-197. Nowak RM (1991) Walker's mammals of the world, 5th ed, vol 2, pp 858-862. Baltimore: Johns Hopkins UP. Plomin R, McClearn GE (1993) Quantitative trait loci (QTL) analyses and alcohol-related behaviors. Behav Genet 23:197-11. Polymeropoulos MH, Xiao H, Sikela JM, Adams MD, Venter JC (1993) Chromosomal distribution of 320 genes from a brain cDNA library. Nat Genet 4:381-386. Purves D (1988) Body and brain. A trophic theory of neural connections. Cambridge: Harvard UP. Rice DS, Williams RW, Goldowitz D (1995a) Genetic control of retinal projections in inbred strains of albino mice. J Comp Neurol 354: 459-469. Rice DS, Williams RW, Harris B, Bailey PW, Davisson MT, Goldowitz D (1995b) Mapping the Bst mutation on mouse chromosome 16: a model for human optic atrophy. Mamm Genome 6:546-548. Rodieck RW, Brening RK (1983) Retinal ganglion cells: Properties, types, genera, pathways and trans-species comparisons. Brain Behav Evol 23:121-164. Roff DA, Mousseau TA (1987) Quantitative genetics and fitness: lessons from Drosophila. Heredity 58:103-118. Romer AS (1969) Vertebrate history with special reference to factors related to cerebellar evolution. In: Neurobiology of cerebellar evolution and development (Llinas R ed), pp 1-18. Chicago: Amer Med Assoc. Ross RA, Judd AB, Pickel VM, Joh TH, Reis DJ (1976) Strain-dependent variation in number of midbrain dopaminergic neurones. Nature 264:654-656. Rubenstein JLR, Martinez S, Shimamura K, Puelles L (1994) The embryonic vertebrate forebrain: the prosomeric model. Science 266:578-580. Scheiner SM (1993) Genetics and evolution of phenotypic plasticity. Ann Rev Ecol Systematics 24:35-68. Scheiner SM, Lyman RF (1989) The genetics of phenotypic plasticity. I. Heritability. J Evol Biol 2:95-107. Selzer ME (1979) Variability in maps of identified neurons in the sea lamprey spinal cord examined by a wholemount technique. Brain Res 163:181-193. Shook BL, Maffei L, Chalupa LM (1985) Functional organization of the cat's visual cortex after prenatal interruption of binocular interactions. Proc Natl Acad Sci USA 82:3901-3905. Silver LM (1995) Mouse genetics. Concepts and applications. New York: Oxford UP. Silver LM (1995) Mouse Genetics. Concepts and Applications. Oxford Univ Press.Smith LA (1928) A comparison of the number of nerve cells in the olfactory bulbs of domesticated albino and wild Norway rats. J Comp Neurol 45:483-499. Sokal RR, Rohlf FJ (1981) Biometry. 2nd ed. New York: WH Freeman Co. Snedecor GW, Cochran WG (1980) Statistical methods. 7th ed. Ames Iowa: Iowa State UP. Stent GS (1981) Strength and weakness of the genetic approach to the development of the nervous system. Ann Rev Neurosci 4:163-194. Stent GS (1981) Strength and weakness of the genetic approach to the development of the nervous system. Annu Rev Neurosci 4:163-Stevens CF (1994) Complexity of brain circuits. In: Complexity: metaphors, models, and reality. (Cowan G, Pines D, Meltzer D eds) pp 245-261. Reading PA: Addison-Welsey. Strom RC, Williams RW, Goldowitz D (1995) Developmental mechanisms responsible for strain differences in the retinal ganglion cell population. Soc Neurosci Abst 21:1523. Sutcliffe JG (1988) mRNA in the mammalian central nervous system. Ann Rev Neurosci 11:157-198. Takahashi JS, Pinto LH, Vitaterna MH (1994) Forward and reverse genetic approaches to behavior in the mouse. Science 1724:1724-1733. Taylor B (1978) Recombinant inbred strains: Use in gene mapping. In: Origins of inbred mice (Morse H, ed), pp 423-438. New York: Academic. Taylor B (1989) Recombinant inbred strains. In: Genetic variants and strains of the laboratory mouse. (Lyon MF, Searle AG eds), pp 773-789. New York: Oxford UP. Tejedor F, Zhu XR, Kaltenbach E, Ackermann A, Baumann A, Canal I, Heissenberg M, Fischbach KF, Pongs O (1995) minibrain: A new protein kinase family involved in postembryonic neurogenesis in Drosophila. Neuron 14:287-301. Thorn RS, Truman JW (1994) Sexual differentiation in the CNS of the mouth, Manduca sexta. I. Sex and segment-specificity in production, differentiation, and survival of the imaginal midline neurons. J Neurobiol 25: 1039-1053.Tukey JW (1977) Exploratory data analysis. Reading MA: Addison-Wesley. Usui H, Falk JD, Dopazo A, de Lecea L, Erlander MG, Sutcliffe JG (1994) Isolation of clones of rat striatum-specific mRNAs by directional tag PCR subtraction. J Neurosci 14:4915-4926. Vogel F, Motulsky AG (1986) Human genetics, problems and approaches. 2nd ed. Berlin: Springer. Waddington CH (1956) Genetic assimilation of the bithorax phenotype. Evolution 10:1-13.Waddington CH (1957) The strategy of the genes. London: Allen and Unwin. Wahlsten D (1983) Maternal effects on mouse brain weight. Dev Brain Res 9:215-221. Wahlsten D (1992) The problem of test reliability in genetic studies of brain-behavior correlation. In: Techniques for the genetic analysis of brain and behavior: focus on the mouse (Goldowitz D, Wahlsten D, Wimer RE eds), pp 407-422. Amsterdam: Elsevier. Wayne RK, Modi WS, O'Brien SJ (1986) Morphological variability and asymmetry in the cheetah (Acinonyx jubatus), a genetically uniform species. Evolution 40:78-85. Wetts R, Herrup K (1982) Cerebellar Purkinje cells are descended from a small number of progenitors committed during early development. Quantitative analysis of lurcher chimeric mice. J Neurosci 2:1494-1498. Williams GC (1992) Natural selection. Domains, levels, and challenges. New York: Oxford UP. Williams MA, Pi–on, LGP, Linden R, Pinto LH. (1990) The pearl mutation accelerates the schedule of natural cell death in the early postnatal retina. Exp Brain Res. 82:393-400. Williams RW, Bastiani MJ, Lia B, Chalupa LM (1986) Growth cones, dying axons, and developmental fluctuations in the fiber population of the cat's optic nerve. J Comp Neurol 246:32-69. Williams RW, Herrup K (1988) The control of neuron number. Ann Rev Neurosci 11:423-453. Williams RW, Rakic P (1988a) Elimination of neurons from the rhesus monkey's lateral geniculate nucleus during development. J Comp Neurol 272:424-436. Williams RW, Rakic P (1988b) Three-dimensional counting: an accurate and direct method to estimate numbers of cells in sectioned material. J Comp Neurol 278:344-352. Williams RW, Goldowitz D (1992b) Lineage versus environment in embryonic retina: A revisionist perspective. Trends Neurosci 15:368-373.Williams RW, Cavada C, Reinoso-Su‡rez F (1993) Rapid evolution of the visual system: A cellular assay of the retina and dorsal lateral geniculate nucleus of the Spanish wildcat and the domestic cat. J Neurosci 13:208-228. Wimer RE, Wimer CC (1985) Animal behavior genetics: a search for the biological foundation of behavior. Ann Rev Psychol 36:171-218. Wimer RE, Wimer CC (1989) On the sources of strain and sex differences in granule cell number in the dentate area of house mice. Dev Brain Res 48:167-176. Wimer RE, Wimer CC, Roderick TH (1969) Genetic variability in forebrain structures between inbred strains of mice. Brain Res 16:257-264. Wimer RE, Wimer CC, Vaughn JE, Barber RP, Balvanz BZ, Chernow CR (1976) The genetic organization of neuron number in Ammon's horns of house mice. Brain Res 118:219-243. Wimer RE, Wimer CC, Vaughn JE, Barber RP, Balvanz BZ, Chernow CR (1978) The genetic organization of neuron number in the area dentata of mouse mice. Brain Res 157:105-122. Wimer RE, Wimer CC, Alameddine L (1988) On the development of stain and sex differences in granule cell number in the area dentata of house mice. Dev Brain Res 42:191-197. Wright S (1978) Evolution and the genetics of populations. Vol 4. Variability within and among natural populations. Chicago: Univ Chicago Press. Yablokov AV (1974) Variability of mammals. New Delphi: Amerind Publ Co.
Since 11 August 98
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Neurogenetics at University of Tennessee Health Science Center
| Print Friendly | Top of Page |
Mouse Brain Library | Related Sites | Complextrait.org
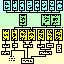 Figure 1:
Mouse lineage chart (74 KB; updated June 96)
Figure 1:
Mouse lineage chart (74 KB; updated June 96)