Note to the Reader Please cite this work as: Williams RW, Gu J, Qi S, Lu L (2001) The genetic structure of recombinant inbred mice: High-resolution consensus maps for complex trait analysis. Genome Biology in press. This preprint accompanies the BXN RI dataset, release 1 of January 15, 2001   The genetic structure of recombinant inbred mice: High-resolution consensus maps for complex trait analysis Robert W. Williams, Jing Gu, Shuhua Qi, and Lu Lu Center for Neuroscience Center for Genomics and Bioinformatics University of Tennessee, 855 Monroe Avenue, Memphis, Tennessee 38163 USA Email questions and comments to rwilliam@nb.utmem.edu and lulu@nb.utmem.edu   Contents Introduction Methods      PCR Procedures      Markers and Databases      Table 1: Number of Loci per Chromosome      Error Checking Procedures Results and Discussion      Recombination densities of RI Strain Sets      Genetic Similarity of RI Strains      Length of RI Genetic Maps      Information Content of RI Sets      Changes in Locus Order      Segregation Distortion in RI Sets      Non-syntenic Association      Residual Heterozygosity      DATA FILES     ABSTRACT Recombinant inbred (RI) strains of mice are an important resource used to map and analyze complex traits. In this study we have increased the density of microsatellite markers 2- to 5-fold in each of several major RI sets that share C57BL/6 as a parental strain (AXB, BXA, BXD, BXH, and CXB). Genotypes of more than 100 RI strains were extensively error checked and regenotyped. A set of 490 markers that were typed in all constituent RI sets were used as anchor loci to assemble high-resolution framework maps. The final consensus maps are based on 1578 microsatellite loci and these maps have a cumulative length of approximately 1400 cM after adjustment for recombination frequencies of RI strains.      Genomes of individuals strains typically incorporate 45–55 recombinations between parental chromosomes. The composite RI set, termed the BXN set, contains 4790 recombination breakpoints. The occurrence of breakpoints conforms to a Poisson distribution with a mean of 1.9 to 3.5 recombinations per chromosome. Distances between breakpoints average 0.5 cM. Approximately 90% of breakpoints have been defined with a precision of better than ±2 cM. Consensus BXN chromosomal maps are close to the length predicted by the Haldane-Waddington equation and are typically 3.6 times longer than single generation meiotic maps. Only a small number of genomic regions in the BXN set deviate significantly from the expected 50:50 segregation ratio of alleles. Genetic correlations between loci on different chromosomes can be high and can generate false positive linkage. We provide two-locus correlograms that can be used to detect and correct for non-syntenic association and to reduce error rates in QTL mapping studies that exploit RI strains.     Introduction Recombinant inbred (RI) strains have been used to map a wide range of Mendelian loci and quantitative traits (Taylor, 1989). They offer compelling advantages for mapping complex genetic traits, particularly those that have low heritabilities. Each recombinant genome is replicated in the form of an entire isogenic line (Bailey, 1981; Belknap, 1998; Crabbe et al., 1999; Toth and Williams, 1999; Hain et al. 2000) and variance associated with environmental factors and error can be suppressed to very low levels. This effectively elevates heritability and greatly improves prospects for mapping quantitative trait loci (QTLs). Recently, RI strains have also been used to map QTLs that that are responsible for biometric variation in the architecture of the mouse CNS (Belknap et al., 1991; Hitzemann et al., 1998; Williams et al., 1998; Strom, 1999; Williams et al., 2000; Lu et al., 2000; Airey et al., 2000). The main advantage in this context is that the complex genetic and epigenetic correlations among interconnected parts of the brain can be explored using complementary molecular, developmental, structural, pharmacological, and behavioral techniques. Gene effects can also be tested under a spectrum of environments and using numerous experimental perturbations. RI strains can therefore be exploited to expose gene-environment interactions. In contrast, interactions between genes and the environment cannot usually be studied using conventional mapping populations in which each animal is unique.      A third advantage of RI strains is that genotypes generated by different groups using a variety of methods can be pooled to generate high-density linkage maps. As a result, loci that segregate in RI sets can often be mapped with impressive precisions without genotyping. This attribute was a significant advantages before the advent of efficient and easy PCR genotyping methods (Weber and Broman, 2000). Unfortunately, over the last ten years databases of RI genotypes have accumulated a high frequency of errors. Each typing error expands distances between loci and degrades linkage between neighboring markers, inevitably blurring associations between genotypes and phenotypes and making it difficult to map underlying loci; whether Mendelian or quantitative. The accumulation of false recombinations has become extreme in some RI sets. For example, the map of Chr 1 in the complete BXD dataset (Mouse Genome Informatics release 2.5: www.informatics.jax.org/searches/riset_form.shtml) is made up of 160 linked loci and is an astonishing 1305 cM long. This map is approximately 12 times the length of an F2 map of Chr 1, and just over 3 times the length expected of an RI map of Chr 1. The accumulation of errors has led to efforts to reconstitute maps using curated subsets of markers for which genotypes can be adequately and independently verified. Sampson and colleagues (1998) assembled maps for the AXB and BXA recombinant inbred stains that improved the utility of this set. Taylor and colleagues (1999) have assembled comparable high quality maps for the complete set of 36 BXD strains that are based almost entirely on easily typed and verified microsatellite markers.      Our study has aims that complement these previous efforts. Our first aim has been to generate reliable high-resolution genetic maps for five widely used sets of RI strains: AXB, BXA, BXD, BXH, and CXB. These strain sets all share C57BL/6 alleles and they can be assembled into a "BXN" superset consisting of just over 100 lines. To asssemble this BXN composite we genotyped all RIs using 490 common microsatellite markers. We intercalated data from an additional 1100 microsatellite markers that had been typed in one or more of the constituent RI sets by us or by other investigators. The new genetic maps we have generated have comparatively high resolution and low error rates and they will be useful in mapping complex traits. Our second aim has been to describe the recombination characteristics of typical RI strains and their chromosomes in a more theoretical context. We have empirically tested the Haldane-Waddington equation of map expansion in sib-mated RI strains; we have tested relatedness among RI lines, and we have measured deviations from Hardy-Weinberg equilibrium associated with 20–30 years of inbreeding, genetic drift, mutation, and selection. Our third aim has been to help to resolve a problem in QTL mapping that arises from non-syntenic genetic correlations within mapping panels. Genetic correlations between intervals on different chromosomes can be high in RI sets. This can result in spurious results and false positive QTLs. We provide detailed correlation matrices that can be used to detect and control for non-syntenic association.   Material and Methods Strains and DNA. Genomic DNA for many strains was purchased from the Jackson Laboratory (www.jax.org). DNA was obtained from 40 of 41 AXB and BXA strains and 35 of 36 BXD strains, 12 BXH strains, and 13 CXB strains. For visual clarity in this paper we have dropped hyphens and substrain designations from RI strain names. For example, strain BXD-1/Ty is referred to as BXD1. Databases and web-accessible data tables at www.nervenet.org also use this simplified nomenclature. Formal strain and substrain symbols of these strains are available at jaxmice.jax.org/html/infosearch/pricelistframeset.html.      DNA from the Jackson Laboratory Mouse DNA Resource was extracted from single male mice. The RI animals that we genotyped were with a few exceptions the progeny of more than 20 serial matings between siblings. Data on the particular generation that we used for genotyping and the current generation of RI animals are listed in a one of several web-accessible tables that accompany this publication (AXB and BXA, BXD, BXH, and CXB). DNA from the 13 CXB strains and from seven new BXH strains generated by Dr. Linda Siracusa (Thomas Jefferson Medical College, Philadelphia) was extracted from spleen using a high salt procedure (Laird et al., 1991, PCR.html). The new BXH strains were generated by crossing C57BL/6J-<c2J/c2J> albino males with C3H/HeJ females and their production and genotyping will be described in detail elsewhere (L Siracusa and RW Williams, in preparation). Three of the new BXH albino strains are no longer available (C2, D1, and E2). We genotyped 107 RI strains. Several sets of RI strains are genetically related. We deleted three non-independent strains from most of our analysis: AXB18, ABX20, and BXA17.      We refer to the collected RI set as the BXN set because each strain includes C57BL/6 (B6 or B) as one of the parental strains—the common substrain C57BL/6J in the case of AXB, BXA, BXD, and BXH; and the substrain C57BL/6By in the case of CXB. The other parental strain in the BXN set is not B6-derived: A/J in both AXB and BXA sets, DBA/2J in BXD, C3H/HeJ in BXH, and BALB/cBy in CXB. PCR Procedures Microsatellite loci distributed across all autosomes and the X chromosome were typed using a modified version of the protocol of Love and colleagues (1990) and Dietrich and colleagues (1992) described in detail at www.nervenet.org/papers/PCR.html. A total of 1773 primer pairs (MapPairs) that selectively amplify polymorphic MIT microsatellite loci were purchased from Research Genetics (www.resgen.com). Each 10 µl PCR reaction mixture contained 1X PCR buffer, 1.92 mM MgCl2, 0.25 units of Taq DNA polymerase, 0.2 mM of each deoxynucleotide, 132 nM of the primers, and 50 ng of genomic DNA. Reactions were set up using a 96-channel pipetting station. A loading dye (60% sucrose, 1.0 mM cresol red) was added to the reaction before the PCR (Routman et al., 1994). PCRs were carried out in 96-well microtiter plates. We used a high-stringency touchdown protocol in which the annealing temperature was lowered progressively from 60 °C to 50 °C in 2 °C steps over the first 6 cycles (Don et al., 1991). After 30 cycles, PCR products were run on cooled 2.5% Metaphor agarose gels (FMC Inc., Rockland ME), stained with ethidium bromide, and photographed. Gel photographs were scored and directly entered into relational database files.      Eighteen primer pairs were resynthesized at our request by Research Genetics using the original sequence data (Whitehead/MIT SSLP Release 16) to verify that our chromosome reassignments of microsatellite loci were not due to the use of incorrect primer sequences. In two cases (D12Mit167 and D3Mit252) the resynthesized primers were compatible with the original assignment made by Dietrich and colleagues rather than our reassignment. In the remaining 16 cases, our reanalysis with new primers confirmed our provisional reassignments. Four loci have the suffix UT appended to their names or symbols. These are loci that were mapped using existing primer pairs obtained from Research Genetics, but which are not positionally related to the original MIT locus. D12MIt167UT, for example, is a locus that has a unique strain distribution pattern that unequivocally maps to proximal Chr 10 using the first set of primers that we obtained from Research Genetics. The other UT loci are D7Mit25UT (Chr 17), D19Mit46UT (Chr 14), and D3Mit252UT (Chr 11). Common Markers. Databases. Relational database files were assembled from the 2000–2001 chromosome committee reports, the Portable Dictionary of the Mouse Genome (Williams, 1994, www.nervenet.org), and the MIT/Whitehead SSLP database Release 16. These files contain a summary of information on chromosomal positions of over 6500 microsatellite markers and information on an additional 20000 genes and markers. We have included Nuffield Department of Surgery (Nds) microsatellite markers for which primer sequences are available. Additional databases devoted to each RI set were assembled from text files downloaded from the Mouse Genome Database. New and corrected genotypes were entered directly into these files.      Table 1 summarizes the number of microsatellite markers that we generated and collected for each set of RI strains on each chromosome. In the case of the AXB-BXA strains we pooled our genotypes with those generated by Sampson and colleagues (1998). Our new BXD data were pooled with genotypes of Taylor and colleagues (1999), and CXB genotypes were pooled with the genotypes of Panoutsakopoulou and colleagues (1997). All data were eventually transferred to Map Manager QT and QTX. Both individual RI databases and the composite BXN database are available as text files formatted for used with Map Manager QTX files at www.nervenet.org/papers/images/DataList.html. The text files are compatible with Windows and Macintosh versions of Map Manager QTX and can of course be imported into a text editor or spreadsheet program.        In general, we retained the order of microsatellite loci listed either in the Chromosome Committee Reports or in Releases 8 to 16 of the MIT/Whitehead microsatellite database. Markers were frequently reordered over short distances to maximize linkage LOD scores using the full BXN set. It is possible to reorder loci in single RI sets to obtain subset-specific improvements in LOD score, but this will introduce equal of greater numbers of recombinations in other members of the BXN set. Full genomic sequence data will soon make it possible to obtain definitive locus order and to fully integrate microsatellite maps with the physical maps of C57BL/6J chromosomes. Calculation of chromosome map lengths . We computed the total numbers of crossovers per chromosome to obtain an estimate of total chromosome length (Table 3). This procedure will be biased to the extent that double recombinantion events over short intervals are not detected. However, marker density is sufficiently high that the number of undetected recombinations is low. To compute the approximate length of intervals between adjacent makers we used an algorithm implemented in Map Manager QT. Map Manager QT counts all unambiguous recombinations in intervals between sequential markers. It then counts the number of crossovers that cannot be unambiguously assigned to a single interval due to incomplete marker data (Table 2). This second count is apportioned on a fractional basis to each interval in proportion to the number of unambiguous recombinations. The apportionment of ambiguously positioned crossovers is then recomputed iteratively until estimated numbers of crossovers converge to stable recombination fractions. Finally, Map Manager applies the Haldane-Waddington equation to calculate the equivalent recombination fraction for a single-generation cross. Error checking. To minimize genotyping errors we retyped a large number of markers, particularly those that were associated with unusually large numbers of recombination events. We were particularly interested in minimizing the number of genotypes that appeared to be associated with two closely apposed recombination events—what are sometimes referred to as double recombinant haplotypes. These double recombinants appear to result from two separate crossover events, one of which is just proximal to a particular marker, the other of which is just distal to that marker. For example the haplotype of a short chromosome interval, -B-B-B-B-N-B-B-B-B-, is associated with two recombinations that flank the central marker with the N genotype. Because of interference, the occurrence of two recombinations within 10 cM is highly improbable in an F2 intercross and consequently, double recombinants are often used estimate genotyping error rates or incorrect marker order. However, recombination events accumulate over many generations in an RI strain and interference is not a factor. Two or more recombinations can be extremely close to each other and can produce true double recombinant haplotypes. It is therefore necessary to verify all apparent double recombinants in RI strains. We checked our own marker genotypes and the majority of markers typed previously by other investigators if they were associated with double recombinants in one of more RI strain. When two or more strains contributed to double recombinants we usually retyped all strains at that marker. Approximately 150 double recombinant haplotypes (and 300 false recombinations) were eliminated in the process of error checking. In a few instances our alternations have actually generated new double recombinant haplotypes.      Error checking is complicated to a limited extent by the fixation of aberrant allelic variants within recombinant inbred strains. We discovered unexpected polymorphisms at the following loci in several lines and all were scored as unknown (U). Marker cM Strains N (bp) B (bp) observed (bp) D6Mit61 53.0 AXB13, AXB14 146 136 142 D6Mit116 6.0 AXB13, AXB14 114 123 108 D15Mit175 6.7 AXB1, AXB3 164 178 140 D6Mit264 3.2 CXB6, CXB12 116 124 120 D9Mit162 28.5 BXH2, 3, 6, 8 122 140 118        The clustering of aberrant products in AXB13 and AXB14 is consistent with the common origin of these strains from a partly inbred progenitor line. However the genotypes of the other three sets of strains (e.g., AXB1 and AXB3) are generally completely independent.      PCR primer pairs in several intervals gave two bands consistent with a genuine heterozygous haplotypes. Heterozygous markers were rare among the fully inbred RI strains but were fairly common among the seven new BXH strains that were only at the tenth to 16 generation when we obtained samples in 1997. In scoring recombination frequency we treated all heterozygous loci and intervals as if they had not been typed. Mutations in microsatellite loci may be responsible for some heterozygosity.     Results and Discussion RI consensus maps of mouse chromosomes When we began this work fewer than 25 microsatellite markers had been typed on each of the four major RI sets. We have increased this to 490 markers. We relied on these loci to assemble consensus RI maps. An additional 986 MIT markers were typed by us and by other groups in at least one set of RI strains. Any pair of RI sets share between 500 and 600 fully genotyped markers. For example, the two largest RI sets—AXB/BXA and BXD—have been typed at 591 common microsatellite markers. The RI maps are based on a total of just under 1600 microsatellite makers (Table 2). The summed length of all chromosomes (Chr Y excepted) is approximately 1413 cM when values are converted from RI recombination frequencies to those expected of typical single-generation maps. The corresponding Chromosome Committee Report (CCR) maps have a cumulative length of 1494 cM between the same markers. The MIT-Whitehead maps have a cumulative length of approximately 1384 cM. The agreement at the whole genome level is excellent.       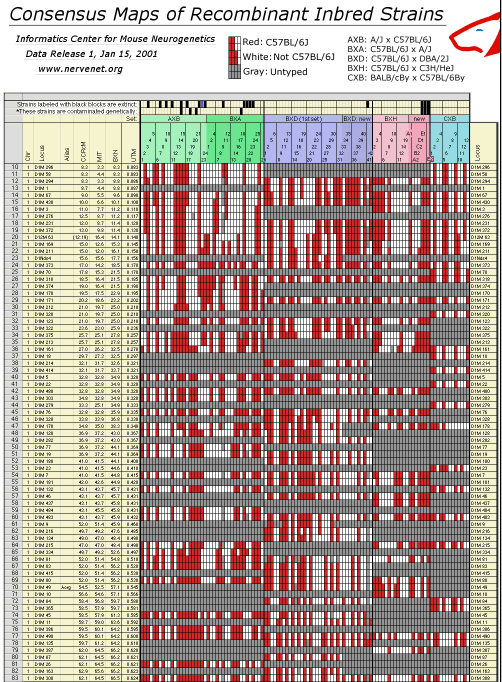Table 2. You may need to assign your browser more memory than usual to dowload this 9-meter-long "wall-paper" format figure in GIF image format. The original data files are also avaiable in standard text format. Column definitions from left to right: Chr: chromosome assignment based on BXN data set. Our assignments differ in a number of cases from those of the Chromosome Committees. Locus: an abbreviated version of the locus symbol. To improve legibility we have truncated D1MitNN to D1M NN. CCR cM: the position of the locus given in the most recent chromosome committee reports (2000 or 2001), MIT: the position of the locus given in databases at the Whitehead Institute, BXN: The position computed from the current RI dataset adjusted for map expansion, UTM: whole genome position in Morgans with a 5 cM buffer between chromosomes. This UTM column can be used to construct whole-genome LOD score plots. Opening this GIF file in Photoshop requires approximately 100 MB of RAM.      Individual maps are based on from 37 markers (Chr X) to 129 makers (Chr 1) per chromosome (Table 1). The mean separation between markers is approximately 1 cM; 0.95 cM using CCR maps as a reference and 0.87 cM using the RI maps themselves. When the 577 markers that do not have unique strain distribution patterns (SDPs) are excluded from this analysis, the average interval size increases to 1.2 cM using CCR maps and 1.4 cM using the RI data. Typical resolution of the RI set for mapping a Mendelian trait will be approximately 1–2 cM. Approximately 90% the mouse genome is currently less than 2 cM from a typed microsatellite marker in the RI set. The asymptotic resolution of the set of BXN strains given an infinitely dense map in which every possible SDP had been discovered would average about 0.3–0.4 cM. There are currently 14 gaps in the microsatellite map of between 5 to 12 cM between adjacent markers. The largest is on proximal Chr 2.   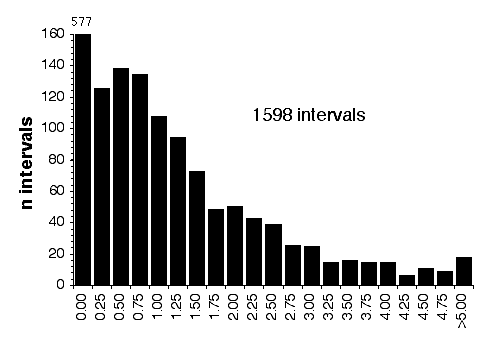Histogram of interval length in centimorgan between microsatellite markers in the BXN set.     Table 3 column definitions: Total SDPs is the total number of unique strain distribution patterns identified in each set. Total R is our estimate of the total number of independent recombinations represented in each complete set of RI strains including members of RI sets that are now extinct. %SDP is our estimate of the percentage of the total number of SDPs that have actually been identified in association with particular markers. This number was computed by dividing "Total SDPs" by "Total R + 20". DR is the sum of recombinations associated with double recombinant haplotypes in each RI set. %DR is the percentage of recombinations associated with these double recombinant haplotypes. R per strain is the estimate of the average number of recombination events accumulated by individual RI strains. *Total number of genetically independent strains per RI set genotyped in this study. The numbers in parentheses is the number of strains available from live stock from the Jackson Laboratory. **Total number of strains per RI set genotyped in this study and all other studies. Of these 109 strains we genotyped 107 (BXA9 and BXD41 were excluded).   This number includes both newly genotyped markers and makers for which genotypes were changed as a result of retyping. # Due to overlap of SDPs this number is not a sum of the overlying four values. The total number of unique SDPs was computed from the composite BXN set directly. Strain independence. Several RI strains share common haplotypes and recombination breakpoints. This duplication or non-independence of RI lines will distort genetic maps. To systematically search for and eliminate partial duplicate RI lines we constructed a genotype similarity matrix for all strains using Qgene (Nelson, 1997). An example of a small part of this matrix is illustrated below for the CXB set. 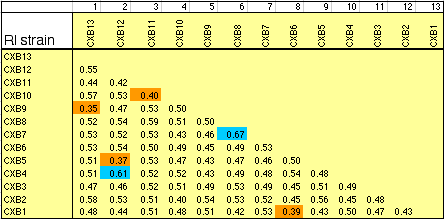Sample of the strain similarity matrix. The fraction of identical genotypes was computed for all two-way combinations of 109 RI strains. Those pairs of strains for which the percentage of shared genotypes was greater than 75% were flagged and one member of the pair was eliminated from the BXN set. Corresponding matrices: AXB-BXA, BXD, BXH and the complete BXN matrix in text format. As already noted by Sampson et al. (1998), three sets of AXB and BXA strains show high genetic similarity: BXA8 and BXA17: 99.8% similar. Only two markers are known to be polymorphic, D3Mit392 and D6Mit108. The polymorphism at D6Mit108 has been verified using independent DNA samples from these two strains. BXA17 is actually a direct derivative of BXA8 separated 1996–1997 (Sampson et al., 1998). Any divergence in genotypes or phenotypes is due to the recent generation and fixation of new mutations in these two separately maintained lines. AXB18, AXB19, and AXB20: 97% to 99% AXB14 and AXB13: 92%         These three sets of strains were treated as three single strains when analyzing recombination frequencies. The mean allele similarity of the remaining strains averages almost precisely 50%. The distribution of values is symmetrical about the mean (Fig. 2) with the great majority of strain pairs falling in the range of 30% to 70% similarity. The highest remaining similarities within RI sets are between BXD13 and BXD41 (74%), AXB6 and AXB17 (73%), BXHB2 and BXH9 (71%), AXB6 and AXB12 (70%), BXD28 and BXD33 (69%), BXD19 and BXD29 (68%), AXB11 and AXB14 (67%). These values are not significantly higher that the similarity scores typically noted across RI sets.   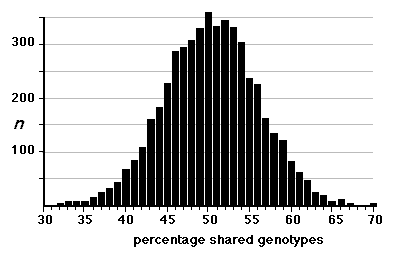Figure 2. Genetic similarity of RI strains. The percentage of identical genotypes was computed for all two-way combinations of 108 RI strains. Those pairs of strains for which the percentage of shared genotypes was greater than 75% were flagged and one member of the pair was eliminated from the BXN set. Map lengths. The mean frequency of recombinations CRI between two linked markers in an RI strain generated by breeding siblings is approximately 4c/(1+6c) were c is the recombination fraction per meiosis (Haldane and Waddington, 1931; Lynch and Walsh, 1998, p 436). An infinitely dense RI map should therefore average four times the length of the conventional one-generation F2 map. Most expansion is achieved in the first few generations, and by F7 the genetic map is approximately three times the length of an F2 map (Fig. 3). The expectation is that a map based on loci spaced at intervals of 1 cM (c = 0.01 in an intercross of backcross) will be expanded approximately 3.66-fold. Similarly, a low-density map based on markers at 16 cM will appear to be expanded 2-fold. F2 and N2 maps generated using uniform typing procedures typically have a cumulative length of 1300 to 1400 cM. Five conventional crosses that we have generated (four F2s and one N2, each genotyped at 91 to 128 loci) average 1320 ± 50 (SEM) cM in length. In comparison the fully error-checked native BXN map is approximately 3.6- to 3.7-fold longer, or a total of 4786 cM. The expansion averages approximately 3.4-fold when the comparison is made to the CCR consensus maps (Table 4). The expansion between common proximal and distal markers ranges from 2.8 in Chr 5 to 3.8 in Chr 12. In general the expansion estimate of 3.6–3.7 agrees extremely well with the Haldane-Waddington expectation given a mean spacing between neighboring markers of about 2–3 cM. The X chromosome only recombines with half the frequency of the autosomes and for this reason its expansion is only 1.8 fold. 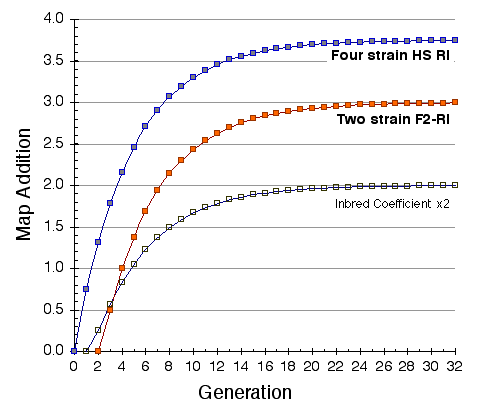Figure 3. Progressive expansion of RI genetic maps during inbreeding. The middle series of points (red) that start at generation 2 shows the addition of map length—and the proportional increase in the numbers of recombination breakpoints—relative to a standard one-generation F2 map. For example, at generation 7, approximately 2 map lengths have been added to the initial map. By F24 the total RI map is almost precisely 4 times as long as a standard F2 map. This same addition characterizes other diallele crosses that start near Hardy-Weinberg equilibrium, including advanced intercrosses. A two strain G8 advanced intercross with a 6000 cM map length would ultimately produce a G8 RI set with map length of 6000 + 3x1400 cM = 10200 cM. The upper series of points (blue) illustrate the accumulation in map length in a four strain intercross at Hardy-Weinberg equilibrium at generation 0. This cross will gain up to 3.75 map equivalents. The lowest set of points is the inbreeding coefficient at each generation.        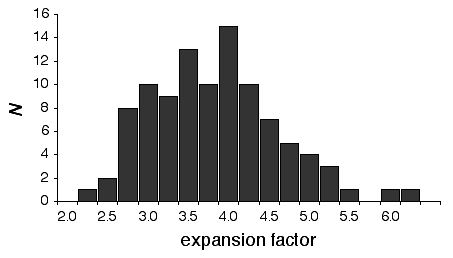There is considerable variation in the average expansion among strains: from a low of 2.24 in BXD40 (the RI strain with the fewest recombinations) to a high of about 6 in BXH6 (Fig. 3). The highly recombinant RI strains will typically be more useful in mapping traits. It would be advantageous to generate RI lines from animals that are more highly recombinant than an F2 generation. By genotyping and selectively breeding more highly recombinant animals it would be possible to generate RI strain sets that significantly exceed the expansion predicted by the Haldane-Waddington equation. A 6x to 8x map should be attainable. Recombination density can also be increased by starting an RI strain using either advanced intercross progeny or heterogenous stock (Fig. 3). Recombination events accumulate additivity across generations and crosses. It is tempting to think that an advanced intercross with a 4x map expansion when used to generate a set of RI lines will experience an additional 4x expansion, or 16x total. This is incorrect. The total expansion of an RI line derived from an 8th generation advanced intercross will be close to 8x if matings are random. Figure 4 Mean expansion of the genetic map in RI strains. The average is approximately 3.7 for 100 independent RI lines. The X axis can also be considered the mean number of recombinations per 100 cM in different RI strains. The x axis can also be transformed into the total number of recombinations per strain by multiplying by the genetic length of the mouse genome in morgans (approximately 14 Morgans; 2.25x = 31.5 recombinations/strain, 3.00x = 42 recombinations/strain, 4.0x = 56 recombinations per strain; and 6.00x = 84 recombinations per strain). *The distance in centimorgans between the most proximal and the most distal markers on each chromosome. The mean number of strains typed at each marker is approximately 100 and thus distances in centimorgans match the actual number of recombination events per chromosome. In the case of the CCR maps we have truncated map lengths to match the most proximal and distal markers genotyped in the BXN set. Strain distribution patterns. We concentrated genotyping efforts on intervals with comparatively low densities of fully typed microsatellite markers or that appeared to harbor large numbers of recombinations between neighboring markers. Our goal in generating a dense map was to discover and verify as many strain distribution patterns (SDPs) as possible in each RI set given available microsatellite primer pairs. The total number of SDPs in each RI set is approximately equal to the number of recombinations defined by a very dense map. Individual RI strains contain an average of 47 recombinations with a range that with few exceptions is between 40 and 60. The 13 CXB strains are associated with a total of 671 recombinations, whereas the set of BXD strains are associated with approximately 1492 recombinations, or just over one recombination per centimorgan on a standard F2 intercross map. These estimates are systematically deflated by a failure to discover recombinations in still sparsely mapped regions (regions where c is as high as 0.1) but are inflated by typing errors and errors of marker order. Based on current marker density we estimate that we have defined from 35% (AXB/BXA) to 59% (CXB) of the total set of SDPs (Table 1). To discover 406 (59%) of the 671 SDPs in the CXB set required 862 selected markers. Recovering the majority of the remaining 300 SDPs could require an additional 500 well placed makers. However, only the small number of strains that have recombinations actually need to be genotyped to fill SDP gaps. The density of informative microsatellite markers is not yet dense enough to define many more SDPs in the BXN set, but once microsatellite maps have been integrated into chromosome sequence databases it will be straightforward to generate additional single nucleotide polymorphisms and microsatellite markers and use them to define all 5000–6000 SDPs in the BXN set. It will then also be possible to refine the positions of recombination breakpoints. To define the remaining SDPs will be an extremely useful addition for mapping both Mendelian and quantitative traits. Locus order. The order of loci of the BXN consensus map generally conforms to that of the chromosome committee reports and the MIT-Whitehead genetic maps (Table 2). In about 130 instances we have changed the local order of loci over short intervals. For example, D1Mit276 and D1Mit231 on proximal Chr 1 do not recombine in the MIT F2 cross, but in the BXN set there is a single recombination between these markers in BXA11 that is most consistent with a reversal of order relative to the chromosome committee report (compare the columns lableled CCRcM, MITcM, and BXNcM in Table 2). The only non-trivial discrepancy was on proximal Chr 15. We reordered approximately 32 loci of Chr 15 to improve linkage statistics. We have not attempted to integrate the BXN data with numerous other mapping panels and it is likely that CCR order will often be well supported by either large mapping panels or rapidly improving physical maps. Full sequence data will soon resolve these minor inconsistencies. 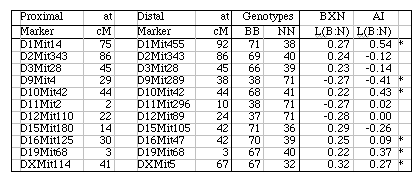Segregation distortion and Hardy-Weinberg equilibrium expectation of allele fixation in RI sets. In the absence of selection approximately 50% of the strains should have inherited B alleles at each marker. A chi-square statistic can be used to assess whether a particular marker has an observed segregation ratio of B and N alleles that differs significantly from expectation. Only the 11 intervals listed below have chi-squared values that are significant at the 0.01 level. Eight of 11 intervals are biased in favor of B alleles. This is most extreme on chromosomes 1, 15, and X, where there are about twice as many strains with B alleles as N alleles. The opposite pattern is seen on chromosomes 9, 11, and 12. Given the large number of comparisons many instances of distortions may be type I statistical errors. We recently genotyped a tenth-generation advanced intercross between C57BL/6J and DBA/2J and it is therefore possible to test whether similar distortion patterns are present in this multigenerational cross. The short answer is that the fixation patterns seen in the BXN are replicated in 6 of 11 intervals. The correlation between ratios of alleles (log of B/N) in these intervals was positive (r = 0.41). It is likely that several of the intervals marked in Table 5 with asterisks represent regions that harbor polymorphic loci that affect fitness.       Table 5: Hardy-Weinberg deviations in the BXN Non-syntenic associations. One important issue in using RI strains for mapping complex traits is that intervals on different chromosomes can become tightly associated or linked in a statistical sense. This non-syntenic association can arise either as a result of random fixation of alleles on different chromosomes during the production of RI strains or can arise as a result of selection for particular combinations of alleles on different chromosomes. Similar patterns of non-syntenic disequilibrium are common in recently admixed human populations and often lead to false positive signals when mapping complex traits. In mice even a modest selection coefficient expressed over 10 generations of inbreeding can generate positive and negative non-syntenic disequilibrium throughout the genome. For example if the combination of B alleles on distal Chr 1 and B alleles on proximal Chr 19 is favorable for fitness then two these intervals will effectively be in linkage disequilibrium in the final RI set. Disequilibrium can also take on the form of strong negative correlations and B alleles may be associated strongly with the group of N alleles. We searched for marked deviations from Hardy-Weinberg two-locus equilibrium by making a series of large correlation matrix of SDPs of pairs of markers. This was done for the entire BXN set and for the constituent RI sets. Table 6 summarizes the most extreme positive and negative correlations among the composite set of 102 independent BXN RI strains. Whether due to chance fixation, selection and epistasis, non-syntenic associations of the sort illustrated in Table 6 are a major source of both false positives and negatives in using RI sets and it is important to examine the correlation matrix once a set of QTLs have been provisionally mapped to see how there summed effects of multiple QTLs disequilibrium will produce spurious QTLs in regions not actually associated with trait variance. 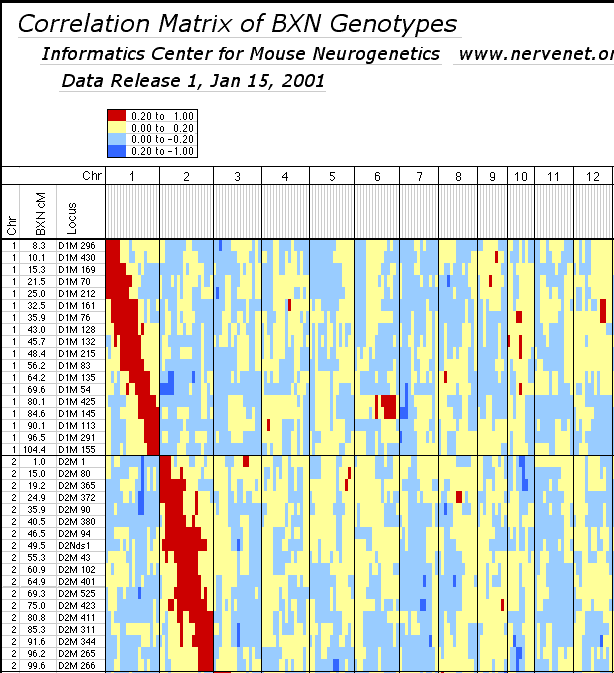Table 6: Correlations of genotypes illustrating non-syntenic associations for 102 strains at 253 loci. This sample from the complete table illustrates both the expected syntenic correlations (large red diagnonal region extending across Chr 1 and Chr 2) and several regions of high non-syntenic correlations between Chr 1 and Chr 2 and other chromosomes. Red regions are linked with positive correlations between 0.20 and 1.0 (p < .05). Darker blue regions are linked with negative correlations of betweeen -0.20 and -0.40 (p < .05). Beige and light blue regions are regions with intermediate correlations that are not statistically diferent from zero with 100 degrees of freedom. For example, the region of Chr 1 near D1Mit425 (labeled D1M 425 in this table) is linked positively to the mid-distal part of Chr 6 and negatively to proximal Chr 7. Tab-delimited text version or Excel version. Controlling for non-syntenic association. Associations among non-syntenic loci can be computed in advance of QTL mapping. It is possible to statistically control for these built-in genetic correlations when mapping by comparing the phenotypes to "residual" genotype values in which non-syntenic linkage has been controlled in a way similar to composite interval mapping. For example, in Table 6 the genotypes at marker D1Mit83 can be partly predicted by genotypes at markers on Chr 7 and Chr 10. D1Mit83 is treated statistically as a dependent variable and markers on Chr 7 and 10 are used as predictors. The residual genotype at D1Mit83 is subsequently used for QTL analysis. Unlike composite interval mapping, the set of controlled loci will vary for each marker and interval. Controlling for non-syntenic correlations will reduce Type I error, but there may be a significant regional loss of power. The process of controlling will introduce blind spots in the genome scan. Intervals that can be almost entirely predicted by combinations of other non-syntenic intervals will effectively be eliminated from a mapping study and QTLs in those intervals may be missed. For this reason it is essential to perform each scan both with and without control for non-syntenic association. The odd situation may arise that a single QTL will need to be assigned initially to two or more physically unlinked chromosomal intervals. Residual heterozygosity. In theory a set of 75,000 genotypes generated across the genome of 100 RI strains should detect only a single residual heterozygous loci at F55 (Fig. 2, fine line; the inbreeding coefficient at F55 is 0.99998812). DNA from most lines was extracted in the 1990s at F generations between F20 and F70 (see Methods and Materials). We detected a total of 10 intervals in nine strains that are heterozygous. Four of these 9 strains are now extinct (BXA20, BXD37, AXB21, and BXA23). DNA samples were taken from single animals of each strain and for this reason these estimates of residual heterozygosity underestimate the total heterozygosity about twofold.       The central part of Chr 1 is interesting because it is still heterozygous in three strains. There is an interval that is approximately 2.5-cM-long that is apparently maintained in heterozygosity in AXB21 on Chr 2. Such maintenance should be accompanied by reduced fecundity in this line if homozygotes are lethal or sublethal. This may account for the poor breeding of this strain and its lack of availability. There is an interval in CXB8 on Chr 1 at 101 cM (D1Mit291 and D1Mit361) that is also heterozygous. It is also possible the heterozygosity is the result of a mutation, but if this were the case we would expect novel length polymorphisms, and in these cases the two alleles were the expected parental length.    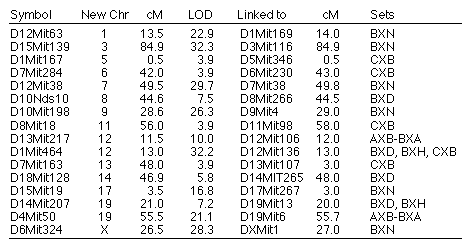Table 7: Loci mapped to unexpected chromosomes Reassigned microsatellite loci. A number of microsatellite loci map to locations on chromosomes other than those expected on the basis of their original assignments (Table 7). Mapping data in one or more of the RI sets is consistent with a reassignments for 16 microsatellite loci to different chromosomes. All of these reassignments are provisional, particularly those with LOD scores less than 10. In several cases, (e.g., D10Nds10) we have reassigned microsatellite loci typed by other investigators that now are linked to new and firmly mapped markers. All primers used to amplify these microsatellites (D10Nds10 excepted) were resynthesizing to confirm that they are identical to those originally specified by Dietrich and colleagues.   Commentary Synopsis The analysis of complex traits using recombinant inbred (RI) strains has been hampered by the modest number of RI strains. Fortunately, five of the most widely used sets of RI strains share C57BL/6 (B) as a parental strain, and it is useful to pool these sets to generate a BXN superset consisting of approximately 100 RI lines. To simplify the use of the BXN set we have increase marker density in all RI lines and have merged the sets using a framework based on 490 shared markers. Approximately 1000 unique strain distribution—an average of almost one per 1.5 cM were discovered and mapped. The cumulative RI map is about 5000 cM in length, or roughly 3.6 times the length of standard intercross or backcross maps. When corrected using the Haldane-Waddington equation the RI maps have a cumulative length of 1400 cM.   Information content of RI strain sets Despite the accumulation of genotypes in RI strains, these genetic resources have still not been typed with sufficient density to accurately define the frequency and positions of recombination breakpoints—to extract the most information from the strain resources. In the venerable set of 13 CXB strains only 11 unique SDPs had been assigned to Chr 1. With a more dense map that is now based on approximately 60 markers we have recovered at total of 37 recombinations on Chr 1, approximately 3 recombinations per strain. The positions of these recombinations has been defined with a precision that ranges from 0.5 to 6.0 cM intervals (2.3 cM average) as referenced to standard CCR maps. Twenty-one of the 38 SDPs are represented by one or more of the marker genotypes, but at least 17 SDPs remain to be defined and these SDP unfortunately cannot be predicted unambiguously. For example, if neighboring markers P and D have the genotypes BBCCC and CCCCC, then there must be at least two recombinations between the markers and there must be at least one unrecovered SDP. We do not know whether the intercalated SDP is BCCCC or CBCCC until we actually type markers in the P–D interval. To discover the missing SDP may require considerable effort especially if available polymorphic markers on the P–D interval have been exhausted. All unrecovered SDPs lower the information content of an RI set. Their absence can significantly reduce linkage of both Mendelian and quantitative traits that are unlucky enough to be controlled by loci in the intervals with ambiguous SDPs. How dense a marker map would be required to define more than 90% of the total number of strain distribution patterns? With 862 markers we were able to define approximately 60% of all likely SDP among the 13 CXB strains. However, in the collected set of BXN RIs only about 25% of the estimated 5000 SDPs have be defined with MIT microsatellites. We can estimate the density of the marker map that would be necessary to define 95% of the SDPs. For example for the BXD set if one assumes a random and independent distribution of breakpoints across strains and a random distribution of markers it would take a map with about 2,700 markers to define 95% of the 1,536 SDPs. Fortunately, the genotyping can be carried out systematically with efforts only directed at intervals very likely to harbor breakpoints. The precision of the maps can be improved in stages with progressively less genotyping in second and third rounds. However, it will be necessary to have access to highly polymorphic makers in critical intervals. Full sequence data of C57BL/6J will make it possible to extract comprehensive lists of polymorphic di- and trinucleotide repeats that can then be rapidly screened. Once QTLs have been mapped to candidate intervals, the subset of strains with recombinations within those intervals become an important resource for confirming and refining QTL location (Darvasi, 1998). This is especially the case if one exploits the RIX method devised by David Threadgill and colleagues. For QTLs or other loci that have already been mapped to a particular chromosome it is useful to have a list of strains in order of their information/recombination content by chromosome. This information can be easily extracted from Table 2 in order to make the appropirate set of RIX F1 intercross progeny to test and refine QTL location. The Potential Power of a QTL Consoritum and Rejoinder to the Commentary in Nature Genetics by Nadeau and Frankel. [Note: This section is an adapted version of a letter by RWW dated Aug 15, 2000.] An important issue is where effort and funding is going to be placed in mouse functional genomics in the next few years. Many geneticists, the DOE, the NIH, and the European mouse genetics community now strongly support large-scale mutagenesis screens. Many researchers are simultaneously involved in complementary QTL studies of specific biologically and clinically important traits. Although QTL research is fairly well supported, this support is distributed widely in the form of smaller grants, and there are currently (2001) no large-scale collaborative QTL programs that match ongoing mutagenesis programs in scope or scale. This as a missed opportunity to build on the strength and expertise of the rapidly expanding international mutagenesis program. After the commentary in Nature Genetics by Joe Nadeau and Wayne Frankel (2000), it may be helpful to reemphasize some of the positive features of QTL analysis. It is also worth redirecting their more pessimistic assessment by pointing out possible solutions to problems they raised, emphasizing how QTL analysis and mutagenesis can work together to increase the yield of genes with known functions. QTL analysis and ENU mutagenesis are both ways to isolate weak alleles that modulate traits. If all we expected of mutagenesis were knockouts or overexpressing lines, we could generate them directly by transgenesis and skip much of the front-end work. QTL analysis has the significant advantage of being targeted at specific biological problems and traits. It also has a somewhat predictable yield of loci per number of genotypes that are phenotyped. All of the massive phenotyping and bioinfomatics skills that are now being applied to mutagenesis can be applied with equal force to systematic QTL analysis. A problem of QTL mapping is that initially stages of analysis are well suited for small research groups (hence, the current R01 structure of support), whereas the later stages of QTL cloning are not (hence, the current frustration of many in this field). High precision QTL mapping requires resources that are not generally available to individual investigatorsÑlarge colonies, high-throughput phenotyping, and significant genotyping requirements. QTL cloning is not an oxymoron, but to prove it, mouse quantitative and molecular geneticists will need to collaborate much more effectively and on a larger scale than we do now. We also need to develop specific genetic resources that will permanently reduce both genotyping and phenotyping burdens. Along these lines, my suggestion is to generate (and expand) several very large sets of recombinant inbred (RI) strains with the goal of producing several sets each with an average map resolution of less than 0.25 cM. This level of resolution would require about 200 conventional RI strains (RIs derived from F2s) or about 50 to 80 advanced RI strains (RIs made from an advanced intercross progeny). Three to six complementary large sets of RIs would allow different QTLs to be harvested for single traits. Each RI set should ideally incorporate more than 6000 breakpoints, giving an average of less than 500,000 base pairs between breakpoints across all autosomes. Generating, genotyping, and phenotyping these strains would require a level of effort equivalent to that of a large mutagenesis project. The RI resources would be permanent and would require relatively modest long-term upkeep given the genetic payback. All data would be cumulative, results could be readily confirmed or refuted, genetic architecture could be explored easily, and even difficult genetic problems, such as norms-of-reaction, maternal effects, and epistasis, could be studied using massive RI intercrosses (RIX). A set of 50 RIs can be converted into 1225 RIX F1s. Combining large RI sets with complementary consomic sets, such as those being made by Joe Nadeau and colleagues, would allow rapid identification of QTLs (using the consomic lines), followed by rapid fine-mapping using the RI and RIX lines. If one wanted to, one could finesse the reciprocal congenic step altogether. The objective of this type of QTL mapping and cloning is the discovery of sets of polymorphic genes associated with well-defined biologically and clinically important heritable traits. The ultimate targets of complex trait analysis are networks of molecules modulated by the polymorphic QTLs, not just the QTL genes individually. There is significant amplification at this stageÑeach QTL is a potential handle on many interacting molecules. It might "only" take 5000 QTLs to get at 50,000 genes. Compared to a reduced "one gene-to-one phenotype" model, complex trait analysis is a somewhat more pragmatic way to think about gene function and the statistical association between alleles and traits.   Acknowledgments This research project was support by a grant from the National Institute of Neurological Disorders and Stroke (R01 NS35485) and as part of the Informatics Center for Mouse Neurogenetics, a Human Brain Project/Neuroinformatics program funded jointly by the National Institute of Mental Health, National Institute on Drug Abuse, and the National Science Foundation (P20-MH 62009). The authors thank Dr. Xiyun Peng for her assistance in genotyping CXB and BXH mice. The authors thank Research Genetics and Ms. Felisha Scruggs for resynthesizing 18 MapPairs for us. We thank Susan Deveau of the Jackson Laboratory DNA Resource for information on the generation numbers of RI DNA samples. We thank Drs. David Threadgill, Gary Churchill, and Kenneth Manly for comments on this preprint.   Data Files: Text, Excel, and Image format Two types of key data are included in the list below in various formats. Items 1 through 4 are versions of the BXN genetic maps and microsatellite marker genotypes. Item 5 includes several different files that present the two-locus correlation matrices of genotypes for different subsets of strains. These correlations matrices are used to detect unsuspected associations between loci on different chromosomes (see main text for an explanation of Non-syntenic Association and the use of the matrices). BXN Database in Map Manager text format (inferred genotypes. Genotype codes: B, N, U, and H, 108 strains) BXN Database in Excel format (original data. Genotype codes: 1 = B, N = 0, Unknown = 2, Het = 0.5) Inferred BXN Database in Excel format (inferred genotypes. Genotype codes: 1 = B, N = 0, Unknown = 2, Het = 0.5). This database is more useful for mapping than the original genotype files. BXN Consensus Maps in GIF image format (this 9-meter-long file may require increased RAM to download)   Correlation Matrices of Genotypes All BXN Genotypes: GIF image format All BXN Genotypes (102 strains): text format All BXN Genotypes (102 strains, 1.1 MB): Excel format BXD Genotypes (34 living strains):text format BXD Genotypes (34 living strains, 1.1 MB): Excel format BXD Genotypes (first 26 strains 1 to 32): text format BXD Genotypes (first 26 strains 1 to 32, 1.1 MB): Excel format CXB Genotypes (13 strains): text format CXB Genotypes (13 strains, 1.1 MB): Excel format AXB Genotypes (24 living and independent strains, 1.1 MB): text format AXB Genotypes (24 living and independent strains, 1.1 MB): Excel format BXH Genotypes: text format BXH Genotypes (1.1 MB): Excel format   Ken Manly's prototype QTL ToolBox: Web-based QTL mapping software for the RI strains   Ken Manly's Map Manager QTX: QTL mapping software for Macintosh OS and Windows     References Airey DC ,Lu L, Williams RW (2001). Genetic control of the mouse cerebellum: identification of quantitative trait loci modulating size and architecture. Journal of Neuroscience, 21:5099–5109. Bailey DW (1959) Rates of subline divergence in highly inbred strains of mice. J Heredity 50:26–30. Bailey DW (1981) Strategic uses of recombinant inbred and cogenic strains in behavior genetics research. In Genetic research strategies for psychogiology and psychiatry. Gershon ES, Matthysse S, Breakefield XO, Ciaranello ED, eds. Plenum NY pp 189–198. Belknap JK (1998) Effect of within-strain sample size on QTL detection and mapping using recombinant inbred strains of mice. Behav Genet 28:29–38. Caldarone B, Saavedra C, Tartaglia K, Wehner JM,Dudek BC, Flaherty L (1997) Quantitative trait loci analysis affecting contextual conditioning in mice. Nature Genetics 17:335–337. Churchill GA, Doerge RW (1994) Empirical threshold values for quantitative trait mapping. Genetics 138:963–971. Darvasi (1998) Experimental strategies for the genetic dissection of complex traits in animals. Nat Gen 18:19–24. Dietrich WF, Katz H, Lincoln SE (1992) A genetic map of the mouse suitable for typing in intraspecific crosses. Genetics 131:423–447. Don RH, Cox PT, Wainwright BJ, Baker K, Mattick JS (1991) ÔTouchdownÕ PCR to circumvent spurious priming during gene amplification. Nucleic Acids Res 19:4008. Hain HS, Crabbe JC, Bergeson SE, Belknap JK (2000) Cocaine-induced seizure thresholds: quantitative trait loci detection and mapping in two populations derived from the C57BL/6 and DBA/2 mouse strains. J Pharmacol Exp Ther 293:180–187. Haldane JBS, Waddington CH (1931) Inbreeding and linkage. Genetics 16:357–374. Haley CS and Knott SA (1992) A simple regression method for mapping quantitative trait loci in line crosses using flanking markers. Heredity 69:315–324. Laird PW, Zijderveld A, Linders K, Rudnicki M, Jaenisch R, Berns A (1991) Simplified mammalian DNA isolation procedure. Nucleic Acids Res 19:4293 Love JM, Knight AM, McAleer MA, Todd JA (1990) Towards construction of a high resolution map of the mouse genome using PCR-analyzed microsatellites. Nucleic Acids Res 18:4123–4130. Lu L, Airey DC, Williams RW (2001) Complex trait analysis of the mouse hippocampus: Mapping and biometric analysis of two novel gene loci that modulate hippocampal size. Journal of Neuroscience, 21:3503Ð3514. Lynch M, Walsh B (1998) genetics and analysis of quantitative traits. Sinauer Associates, Inc. Sunderland, MA. Nelson JC (1997) QGENE: software for maker-based genomics analysis and breeding. Molec Breeding 3:239–245. Panoutsakopoulou V, Spring P, Cort L, Sylvester JE, Blank KJ , Blankenhorn EP (1997) Microsatellite typing of CXB recombinant inbred and parental mouse strains. Mamm Gen 8:357–361. Routman E, Cheverud J (1994) A rapid method of scoring simple sequence repeat polymorphisms with agarose gel electrophoresis. Mamm Genome 5:187–188 Sampson SB, Higgins DC, Elliot RW, Taylor BA, Lueders KK, Koza RA, Paigen B (1998) An edited linkage map for the AXB and BXA recombinant inbred mouse strains. Mamm Gen 9:688–694. Taylor BA (1989) Recombinant inbred strains. In (Lyon ML, Searle AG, eds) Genetic variants and strains of the laboratory mouse 2nd Ed Oxford UP, Oxford. pp 773–796. Taylor BA, Wnek C, Kotlus BS, Roemer N, MacTaggart T, Phillips SJ (1999) Genotyping new BXD recombinant inbred mouse strains and comparison of BXD and consensus maps. Mamm Gen 10(4):335–348. Darvasi (1998) Experimental strategies for the genetic dissection of complex traits in animals. Nat Gen 18:19–24. Weber JL, Broman KW (2000) Genotyping for human whole-genome scans: past, present, and future. Adv in Genet 42:77–96. Williams RW (1998) Neuroscience meets quantitative genetics: Using morphometric data to map genes that modulate CNS architecture. In: Morrison J, Hof P (eds) Short course in quantitative neuroanatomy. Society of Neuroscience, Washington DC, pp 66—78. Williams RW (2000) Mapping genes that modulate mouse brain development: a quantitative genetic approach. In: Mouse brain development. (Goffinet A, Rakic P, eds), pp 21–49. Berlin: Springer. Williams RW, Strom RC, Goldowitz D (1998a) Natural variation in neuron number in mice is linked to a major quantitative trait locus on Chr 11. J Neurosci 18:138–146. Williams RW, Airey DC, Kulkarni A, Zhou G, Lu L (2001) Genetic dissection of the olfactory bulb of mice: QTLs on chromosomes 4, 6, 11, and 17 modulate bulb size. Behavior Genetics 31: 61–77.